正文
3D
到
2D
：
fk-1
是
3
维，
fk
是它们对应的图像上的
2D
重投影。单目相机情况下，
3D
结构需要从
2
个相邻的相机视图（比如
Ik-2
和
Ik-1
）进行三角化，然后和第
3
幅视图中的
2D
图像特征进行匹配（比如，
Ik
）。在单目算法中，需要匹配至少
3
幅视图。
注意，特征可能是点或者线。通常，在无结构的场景中由于缺乏直线，就在视觉里程计中使用点特征。一个深入分析这三种点和线特征方法的论文，在参考论文
74
中可见。本文只讲解点特征的推导。
4.1 2D
到2D：图像特征匹配中的运动
4.1.1 估计本征矩阵
校准过的相机图像
Ik
和
Ik-1
之间的几何关系可以通过本征矩阵
E
表示。
E
中包含了相机运动参数具有一个未知的平移变换因子：
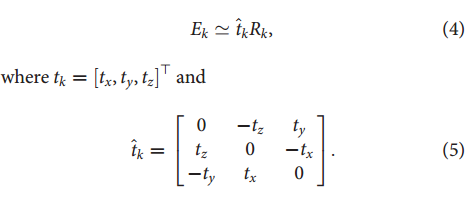
符号
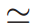表示等式右边是标量乘法。
2D
到
2D
的特征对应关系可以计算本征矩阵，旋转和平移矩阵可以通过本征矩阵进行分解计算。
2D
到
2D
的运动估计最重要的特征是对极约束，它形成一条直线连接两个对应的特征点
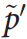和
，
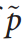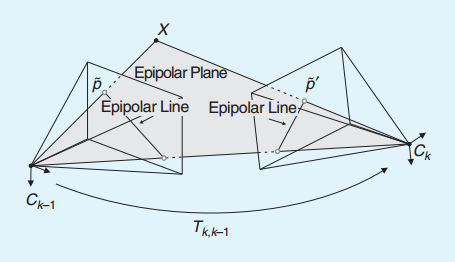
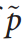是另一幅图像像对应的特征点，如图
4
所示。
这个约束可以通过等式
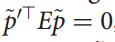推导，其中
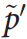是其中一幅图像
Ik
的特征位置，
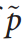是另一幅图像
Ik-1
上对应的特征的位置。
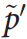和
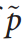的图像坐标是在同一坐标系一致的。
为了简化，我们将归一化的坐标记为
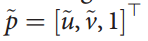，（详细参考“透视相机模型”）。类似的等式，也可以通过单位圆球的归一化坐标推导，（如“圆球模型”所示）。
用对极约束计算
2D
到
2D
特征匹配的本征矩阵。最小化方案是采用
5
个
2D
到
2D
的对应关系，如论文
75
，
Nister
的论文
76
提供了一种实现方法。
Nister
的
5
点算法成为标准的
2D
到
2D
的运动估计方法，包括对离群点的处理。对于
n>=8
的非共面点的一种简单直接的计算方法是
Longuet-Higgins
的
8
点算法，如论文
2
中总结。每个特征匹配都给出一个约束：
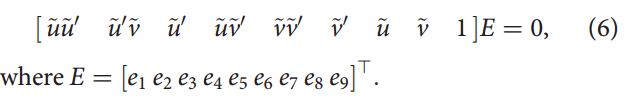
8
点法得到的这些约束进行排列可以得到一个线性方程组
AE=0
，通过解方程，就可以计算出
E
的值。这个齐次方程组可以很容易通过奇异值分解（
SVD
）计算，如论文
2
。如果超过
8
个点会产生超定方程组（方程个数大于未知量个数的方程组），如果超定方程组给定的条件（限制）过于严格，导致解不存在，就用最小二乘法进行拟合，求出最小二乘解，该方法对噪声具有鲁棒性。矩阵
A
的奇异值分解（
SVD
）形式为
A=USV
T
，
E
的最小二乘估计为
||E||=1
可以用
V
的最后一行查找。然而，
E
的线性估计并不满足本征矩阵的特征约束，它是旋转矩阵
R
和反对称平移
t
的乘积。在本征矩阵的奇异值里面可以看到这些约束。经过奇异值分解（
SVD
）分解后的本征矩阵是
E=USV
T
，提取主对角线上值
diag(S)={s,s,0}
，第一个和第二个奇异值相等，第三个是
0
。为了得到满足约束的有效的本征矩阵
E
，需要将它投影到具有有效的本征矩阵的空间中去。投影本征矩阵为
。
当
3
维空间中点共面时，
8
点算法方案退化。相应的，
5
点算法则可以应用于计算共面点。最后，
8
点算法对校准过的（透视或全景）相机和没有校准的相机都可适用，
5
点算法只适用于校准过的（透视或全景）相机。
4.1.2
从本征矩阵E提取旋转矩阵R和平移矩阵t
从计算估计出来的
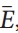中，可以提取旋转和平移矩阵。通常，对同一本征矩阵有
4
种不同的方法求解
R
