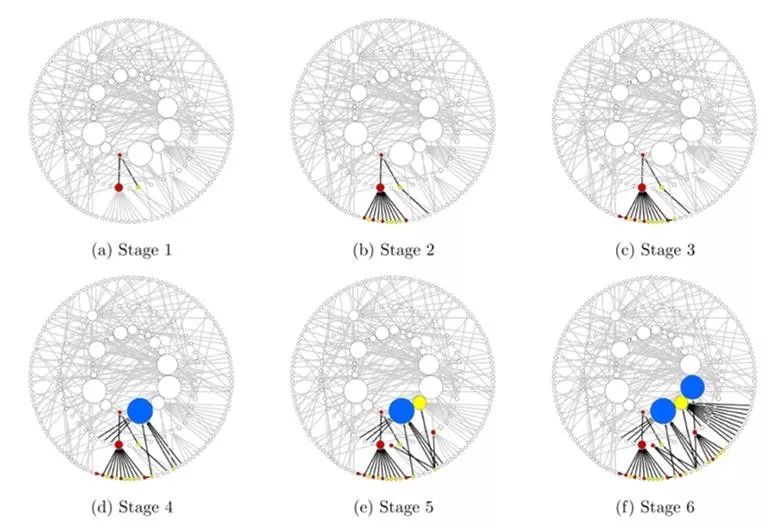
Contagion Network
解析文章首发于唧唧堂网站www.jijitang.com
解析作者 | 唧唧堂经济学小组:
降温
;审校编辑 |
悠悠 糖糖
论文基本信息:
本文是针对论文《银行网络与系统性风险:来自国家银行法案的证据(Bank Networks and Systemic Risk: Evidence from the National Banking Acts)》的一篇论文解析, 该论文于2019年9月发表于《美国经济评论(AER)》杂志上。该研究作者包括Anderson, Haelim(OFR); Paddrik, Mark(OFR); Wang, Jessie Jiaxu(Arizona State University)。
研究背景与问题
2007-2009年的全球金融危机给了我们启示:
个别金融机构的崩溃会引起整个金融系统的危机
。金融机构之间存在交易,整个金融体系因此形成了一个复杂的金融网络。当某个机构陷入危机时,这种风险就会通过网络传染给其他与之间接或直接相连的其他机构,最终可能引起整个系统的崩溃。于是,经济学家们开始研究网络结构和系统性风险之间的关系,但大多数研究从理论出发,即网络结构的构建是通过计算机模拟的方式;由于机构之间交易关系之复杂、变量之多,很难准确地测量金融网络的边,于是极少数的研究是从经验角度,利用微观数据讨论机构间的风险传染。本文通过研究
特定时期(1862-1867)的银行网络
解决了这一数据难题,因为在这个期间银行间交易结构非常简单,用同业拆借数据即可刻画银行网络的拓扑结构。1863-1864年颁布了国家银行法案,这一法案使得美国银行网络的结构发生显著的变化,本文通过1862年与1867年的数据对比,
研究法案颁布对银行网络结构的影响和网络结构变化对系统性风险大小的影响
。
数据与模型
为构建资产负债表,本文利用了两个数据集:Reports of the Several Banks and Savings Institutions of Pennsylvania和National Banks’ Examination Reports,通过作者的计算整合,为每个银行构建如下资产负债表:
左侧是资产,右侧是负债
,第三行的两个变量是银行同业拆解额:

Balance Sheet
1863-1864年颁布的国家银行法案要求地区银行应在中心银行留有一定比例的储备金,使得银行系统呈现以纽约城(NYC)内的银行为中心的三级式机构,法案颁布后这种中心化(右图)更明显:
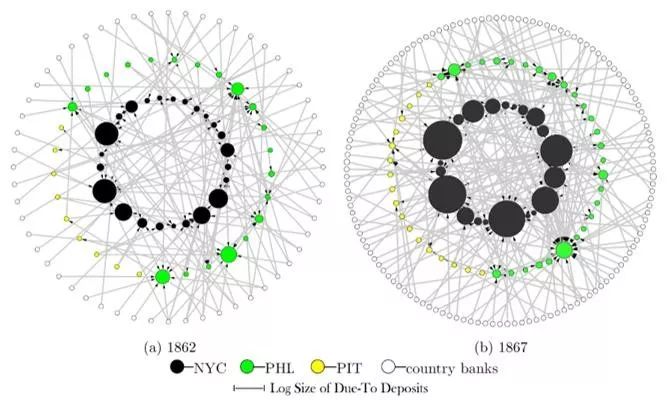
Reserve Hierachy
随后,作者对流动性撤出引起银行清算和破产的机制进行建模,并将模型简化为2期。假设在上方资产负债表中I_i 是t=2到期的长期投资,若在t=1取出需成本 ξ_i I_i,这种高价赎回的行为即预示着银行危机的发生。
假设t=1期有流动性撤出(银行间拆借赎回&储户取款),当银行的现金储备(包括自己和在其他银行的存款)不足时,银行便会进行清算(高价赎回长期投资),即清算条件为:
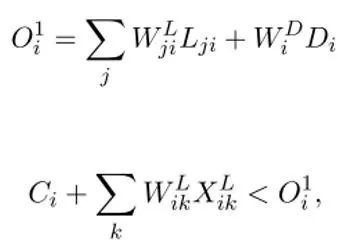
Liquidation Condition
若加上高价赎回长期投资仍不能弥补缺口,银行便会破产,即破产条件为:
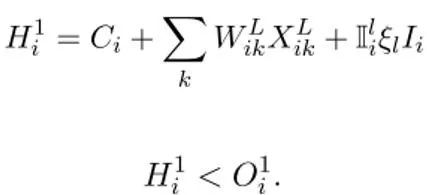
Bankrupt Condition
模拟流动性冲击方法上,作者假设长期投资是风险投资,其收益率是平均收益率加上冲击扰动,即:
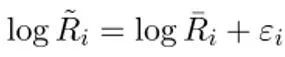
Risky Investment
本文模拟了两种冲击及其对系统性风险的影响,第一种是纽约城内银行的投资损失由上到下传染到其他地区银行(
top-to-bottom
),另一种是某个地区银行的流动性撤出危机由下到上传染到纽约中心地带(
bottom-to-top
)。
研究结论
1.
法案颁布→银行网络中心化程度增加(3级结构)→robust-yet-fragile银行系统
1) 当中心银行受到小的冲击时,更中心化的网络结构使得风险分散能力增强,即更robust;
2) 当中心银行收到大的冲击时,中心化程度更高的网络结构会使得风险扩散到各个地区,导致系统性风险快速上升,即更fragile;
3) 而当地区银行受到无论大还是小的冲击,都可以通过网络结构分散掉。
2. 本文还验证了
清算公司为避免清算发生的借据、暂停兑换这两种应对措施都能够降低系统性风险
。
小编评语:
小编的研究方向是金融计量,所以之前看过一些从分位数回归角度研究金融网络风险传染的文章(Chen, Hardle, & Okhrin, 2019; Härdle, Wang, & Yu, 2016),这类文章更关注估计量的渐近性质,且是reduced-form,即只能看网络相关性作为一个因子是否显著,而不能看具体两两机构之间的传染是怎么发生的,所以AER这篇文章最后给出的dynamics of contagion的网络图(文首)着实美到了我。
虽然基于分位数VAR的计量方法可以做impulse response分析,但是网络的边多是采用common holder/CDS等简化后的变量建立,本文另辟蹊径选择了一个相关结构本来就简单的时期进行分析。
Chen, C. Y. H., Hardle, W. K., & Okhrin, Y. (2019). Tail event driven networks of SIFIs. Journal of Econometrics, 208(1), 282-298.
Härdle, W. K., Wang, W., & Yu, L. (2016). Tenet: Tail-event driven network risk. Journal of Econometrics, 192(2), 499-513.
参考文献:
Anderson, H., Paddrik, M., & Wang, J. J. (2019). Bank Networks and Systemic Risk: Evidence from the National Banking Acts. American Economic Review, 109(9), 3125-61.
解析作者: 降温
点击“阅读原文”,查阅更多作者在唧唧堂的论文解析
搜索关注“
小鹅知识助手
”服务号
一秒进入导读单与小社群





