正文
现实世界不同的领域需要不同的表示方法,比如研究地形分布或者给初来乍到的人指路,最好是画个地图,而非文字说明。类似地,我们通过城市规划图来定位某个建筑,用曲谱记录乐曲。
在分析处理各种抽象的模式和结构时,数学的符号,概念以及程式被证明是最佳的选择。比如我们熟知的加法和乘法的运算律,运用代数符号极其方便有效。我们以加法交换律为例:
(文字形式)两数相加,顺序无关
(代数形式)m+n=n+m
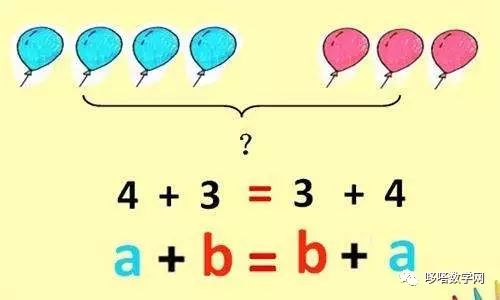
上述例子只是对数学抽象性的惊鸿一瞥。对大部分的数学分支,假如不用抽象的符号,数学将不可避免的繁复。也因此,符号系统伴随数学的发展稳步增长。
符号进入数学,一般归功于法国数学家弗朗西斯·韦达。其实,公元250年亚历山大里亚的丢番图就已经开始使用代数符号。他的十三卷经典《算术》(现存6卷)公认是最早的代数教科书。在书中,丢番图用特殊符号代表未知数,未知数的幂以及减法和等号。
现在的数学书充斥各种符号,但符号之于数学正如乐谱之于乐曲。一段谱子代表一段曲子,谱子只有被唱出来或者演奏出来才成为灵动的曲子,也就是说,乐曲存在于我们的思维中而非纸上。对数学而言,道理也是如此:符号只是数学的表示,当经过专业人员(这里指受过数学训练的人)的解读,抽象的符号有了意义,数学如交响乐一样回响在读者的脑海中。
回到本节开头,再次强调:数学符号的抽象在于数学对象本身的抽象。抽象的数学可以帮助我们理解世界的运行模式。1623年,伽利略写道:
自然这本大书只有掌握它的语言的人方能读懂,这语言就是数学。
事实上,物理学可以用数学语言精确地描述。我们用飞机的例子来说明,数学何以帮助我们理解物理定律。喷气式飞机飞行时,我们是看不到任何向上托它的力量的,只有借助数学,我们才能理解那股隐形的力量。而这股力量,最早由十七世纪的伊萨克·牛顿所研究,经过几个世纪数学和工程的持续发展,我们终于能够制造出实际的飞机。这个例子很好地凸显了数学的力量:让不可见变成可见。
Ⅲ 大学水准的数学
经过前述对数学历史的回顾,现在我们来说明大学数学与中学数学的本质区别。
大约150年前,虽然当时的数学已远远拓展到数之外的范畴,但数学家依旧认为数学的本质是计算,对数学的精通就意味着能够做复杂计算或者熟练推演符号。大体上,中学数学正是在这样的传统观念中建立起来。
直到19世纪,随着数学家攻克更复杂的问题,他们发现直觉并不总是能引导下一步的研究,相反,之前为解决实际问题而发展出来的方法可能会引出违反直觉的结果,比如Banach-Tarski悖论就是一个例子。这个悖论讲的是,理论上,我们可以把一个圆球用某种方式切成小块然后重新组合,就能得到两个(是两个,你没看错)和原来一样大小的圆球。
由此开始,数学迈入了只能在其内部理解自身的新阶段。(因为Banach-Tarski悖论在数学上无懈可击,其结论虽然诡异,我们依旧要承认它)类似上述只能在数学上加以说明而不可能借助其他方式验证的结果,促使数学家用数学方法来检验数学本身。
19世纪中期开始的这种“内省”,让数学家对数学有了全新认识:数学的重心不再是计算求解,而是理解抽象概念和关系,数学由强调“实操”转变为注重“理解”。数学对象不再局限于特定的函数,而是某一抽象性质的载体,证明不仅仅是按照规则变换对象,而是从概念出发进行逻辑推演。
这次观念革命,彻底改变了数学家对数学的看法。然而对数学家之外的人,世界依旧如常。人们真正感觉到变化,是从大学课程开始。比如说你是一个数学专业的大学生,初次接触“新数学”,结果被折磨地死去活来,你很可能会问候狄利克雷,戴德金,黎曼以及所有其他发明这些该死的知识的人。













