正文
:这一点主要强调并行性和通信的重要。由于这方面大家应该比较熟悉,这里不再赘述。
3. Balancing computation with I/O
:平衡运算和I/O,应该说是脉动阵列最重要的设计目标。对于这一点,作者用下面这幅图给出了很好的说明。
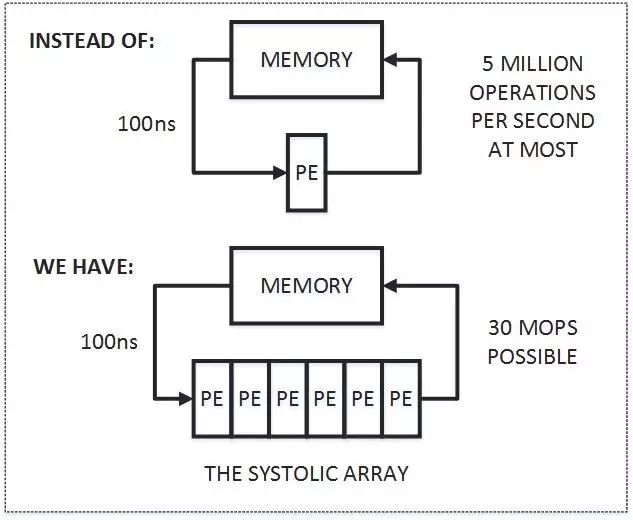
首先,图中上半部分是传统的计算系统的模型。一个处理单元(PE)从存储器(memory)读取数据,进行处理,然后再写回到存储器。这个系统的最大问题是:
数据存取的速度往往大大低于数据处理的速度
。因此,整个系统的处理能力(MOPS,每秒完成的操作)很大程度受限于访存的能力。这个问题也是多年来计算机体系结构研究的重要课题之一,可以说是推动处理器和存储器设计的一大动力。而脉动架构用了一个很简单的方法:
让数据尽量在处理单元中多流动一会儿
。
正如上图的下半部分所描述的,第一个数据首先进入第一个PE,经过处理以后被传递到下一个PE,同时第二个数据进入第一个PE。以此类推,当第一个数据到达最后一个PE,它已经被处理了多次。所以,脉动架构实际上是多次重用了输入数据。因此,它可以在
消耗较小的memory带宽的情况下实现较高的运算吞吐率
。
当然,脉动架构还有其它一些好处,比如模块化的设计容易扩展,简单和规则的数据和控制流程,使用简单并且均匀的单元(cell),避免了全局广播和扇入(fan-in),以及快速的响应时间(可能?)等等。
总结起来,脉动架构有几个特征:1. 由多个同构的PE构成,可以是一维或二维,串行、阵列或树的结构(现在我们看到的更多的是阵列形式);2. PE功能相对简单,系统通过实现大量PE并行来提高运算的效率;3. PE只能向相邻的PE发送数据(在一些二维结构中,也可能有对角线方向的数据通道)。数据采用流水线的方式向“下游”流动,直到流出最后的PE。
到这里不难看出,脉动架构是一种很特殊的设计,结构简单,实现成本低。但它灵活性较差,只适合特定运算。而作者认为,卷积运算是展示脉动架构特点的理想应用,因此在文章中用了很大篇幅介绍了脉动架构实现卷积运算的方法。
首先看看作者对卷积运算的定义:
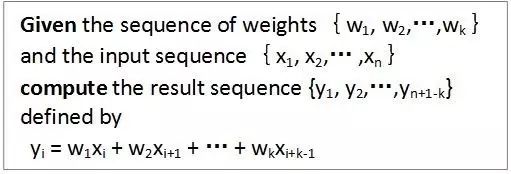
下面是作者给出的一种方法
(
broadcast inputs, move results, weights stay
)
:
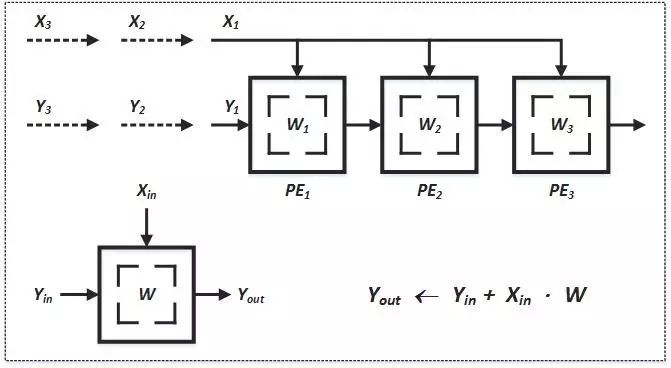
在这个例子中,X值广播到各个运算单元,W值预先存储在PE中并保持不动,而部分结果Y采用脉动的方式在PE阵列间向右传递(初始值为零)。不难看出,经过三个时刻,最右边的PE的输出就是X和W两个序列的卷积运算的第一个结果,这之后就会不断输出Y值。
文中还给出了其它几种实现卷积的方式,如
broadcast inputs, move weights, results stay;fan-in results, move inputs, weights stay
。这几种都算作“
(Semi-) systolic convolution arrays with global data communication
”。另外还有一大类是“
(Pure-) systolic convolution arrays without global data communication
”,包括
results stay, inputs and weights move in opposite directions;results stay, inputs and weights move in the same direction but at different speeds;weights stay, inputs and results move in opposite direction;weights stay, inputs and results move in the same direction but at different speeds
。建议大家好好看看,还是挺有启发的。
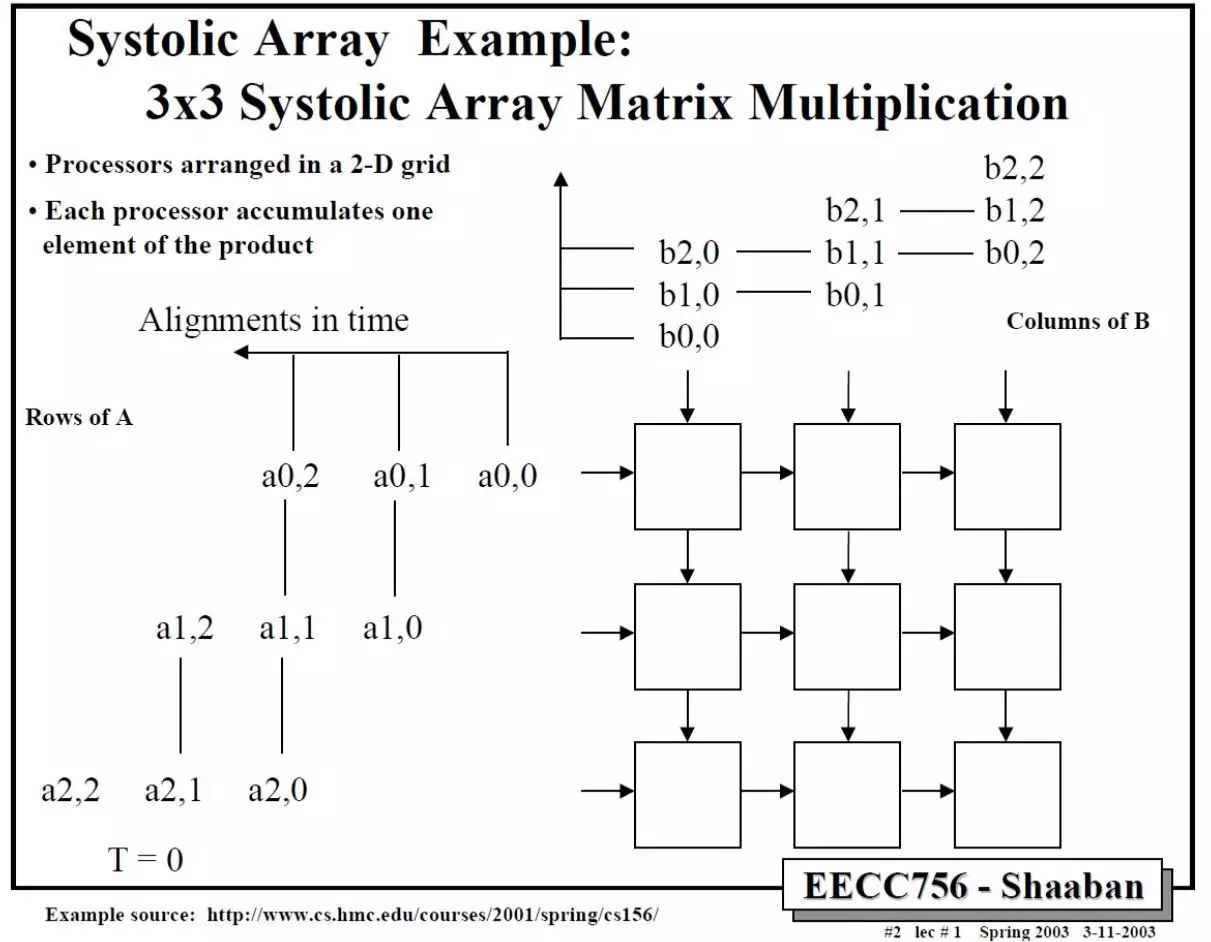
那么二维的脉动阵列如何做矩阵相乘呢?下面这个例子比较清楚。A和B都是3x3矩阵,T表示时刻。