正文
那么我们首先来看一下 CNN 在 Image 当中的应用。如图 3 所示,左图表示的是一张图像在一个神经网络层当中的卷机操作过程。最底部的那一层是输入的特征图(或原图),通过一个卷积(这里表示的是一个 3*3 的卷积核,也就是文章当中的 receptive filed=9)操作,输出一张卷积后的特征图。如图 3 的卷积操作,底层的 9 个像素被加权映射到上层的一个像素;再看图 3 中的右图,表示从 graph 的角度来看左图底层的输入数据。其中任意一个带卷积的区域都可以看作是一个中心点的 node 以及它的领域的 nodes 集合,最终加权映射为一个值。因此,底部的输入特征图可以看作是:在一个方形的 grid 图当中确定一些列的 nodes 来表示这个图像并且构建一个正则化的邻域图(而这个邻域图就是卷积核的区域,也就是感知野)。
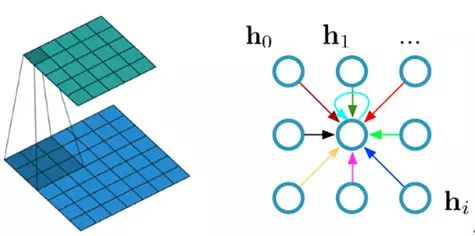
图 3 图像的卷积操作
按照这样的方式来解释,那么如 paper 中 Figure1 所示,一张 4*4 大小的图像,实际上可以表示为一个具有 4 个 nodes(图中的 1,2,3,4)的图(graph),其中每一个 node 还包括一个和卷积核一样大小的邻域(neighborhood filed)。
那么,由此得到对于这种图像(image)的卷积实际上就是对于这 4 个 node 组成的图(graph)的领域的卷积。
那么,对于一个一般性的 graph 数据,同样的只需要选出其中的 nodes,并且求解得到其相关的固定大小(和卷积核一样大小)领域便可以使用 CNN 卷积得到图的特征表示。
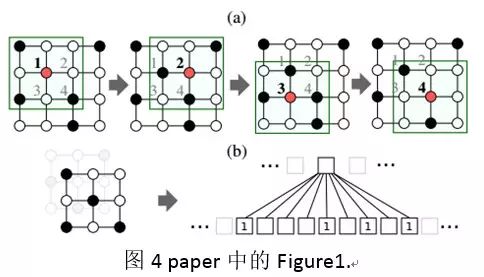
图 4 paper 中的 Figure1
需要注意的是,图 4(b)当中表示的是(a)当中的一个 node 的邻域,这个感知野按照空间位置从左到右,从上到下的顺序映射为一个和卷积核一样大小的 vector,然后再进行卷积。但是在一般的图集当中,不存在图像当中空间位置信息。这也是处理图数据过程当中要解决的一个问题。
基于以上的描述 paper 当中主要做了三个事情:1. 选出合适的 nodes;2. 为每一个 node 建立一个邻域;3. 建立 graph 表示到 vector 表示的单一映射,保证具有相似的结构特征的 node 可以被映射到 vector 当中相近的位置。算法具体分为 4 个步骤:
1. 图当中顶点的选择 Node Sequence Selection
首先对于输入的一个 Graph,需要确定一个宽度 w(定义于 Algorithm 1),它表示也就是要选择的 nodes 的个数。其实也就是感知野的个数(其实这里也就是表明,每次卷积一个 node 的感知野,卷积的 stride= kernel size 的)。那么具体如何进行 nodes 的选择勒?
实际上,paper 当中说根据 graph 当中的 node 的排序 label 进行选择,但是本文并没有对如何排序有更多的介绍。主要采取的方法是:centrality,也就是中心化的方法,个人的理解为越处于中心位置的点越重要。这里的中心位置不是空间上的概念,应该是度量一个点的关系中的重要性的概念,简单的举例说明。如图 5 当中的两个图实际上表示的是同一个图,对其中红色标明的两个不同的 nodes 我们来比较他们的中心位置关系。比较的过程当中,我们计算该 node 和其余所有 nodes 的距离关系。我们假设相邻的两个 node 之间的距离都是 1。














