正文
不同的卷积核提取不同的特征(图片来自互联网)
多幅特征图可以看成是同一张图像的不同通道,这个概念在后面代码实现的时候用得上。
4. 池化
得到特征图之后,可以使用提取到的特征去训练分类器,但依然会面临特征维度过多,难以计算,并且可能过拟合的问题。从图像识别的角度来讲,图像可能存在偏移、旋转等,但图像的主体却相同的情况。也就是不同的特征向量可能对应着相同的结果,那么池化就是解决这个问题的。
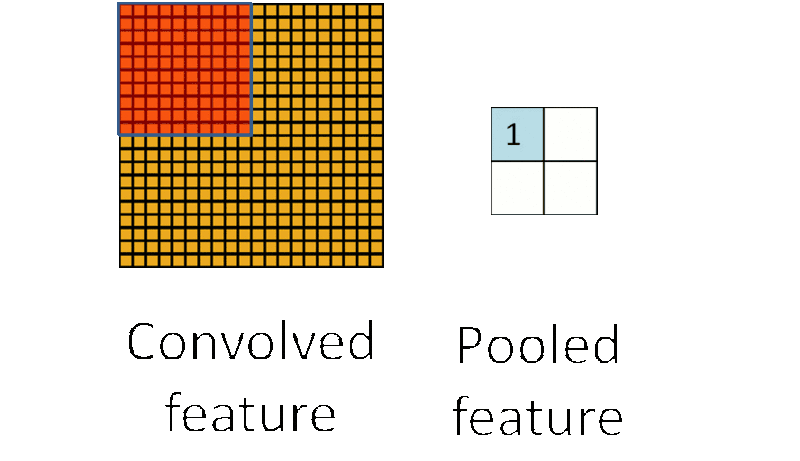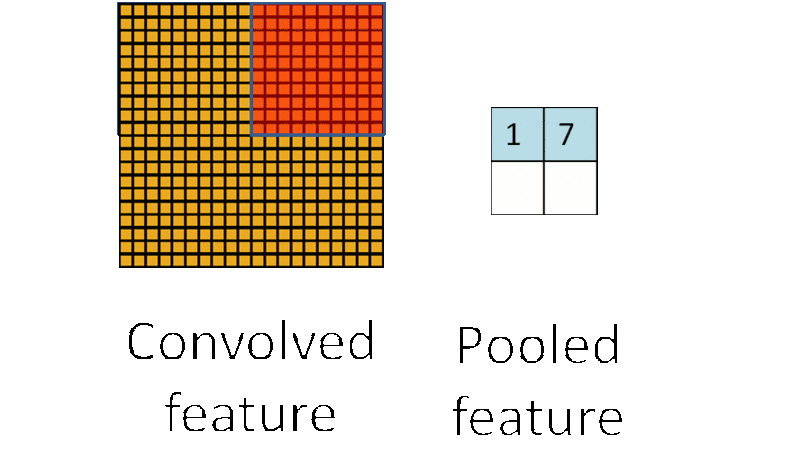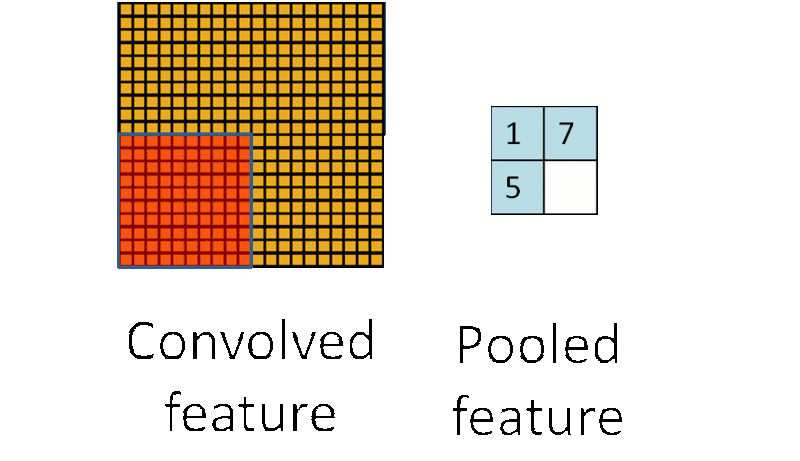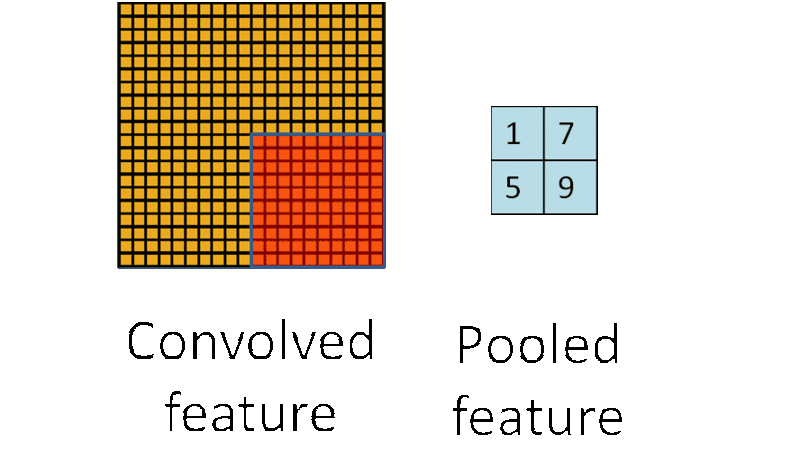
池化过程(图片来自互联网)
池化就是将池化核范围内(比如2*2范围)的训练参数采用平均值(平均值池化)或最大值(最大值池化)来进行替代。
终于到了展示模型的时候,下面这幅图是笔者手画的(用电脑画太费时,将就看吧),这幅图展示了本文中用于训练游戏所用的卷积神经网络模型。
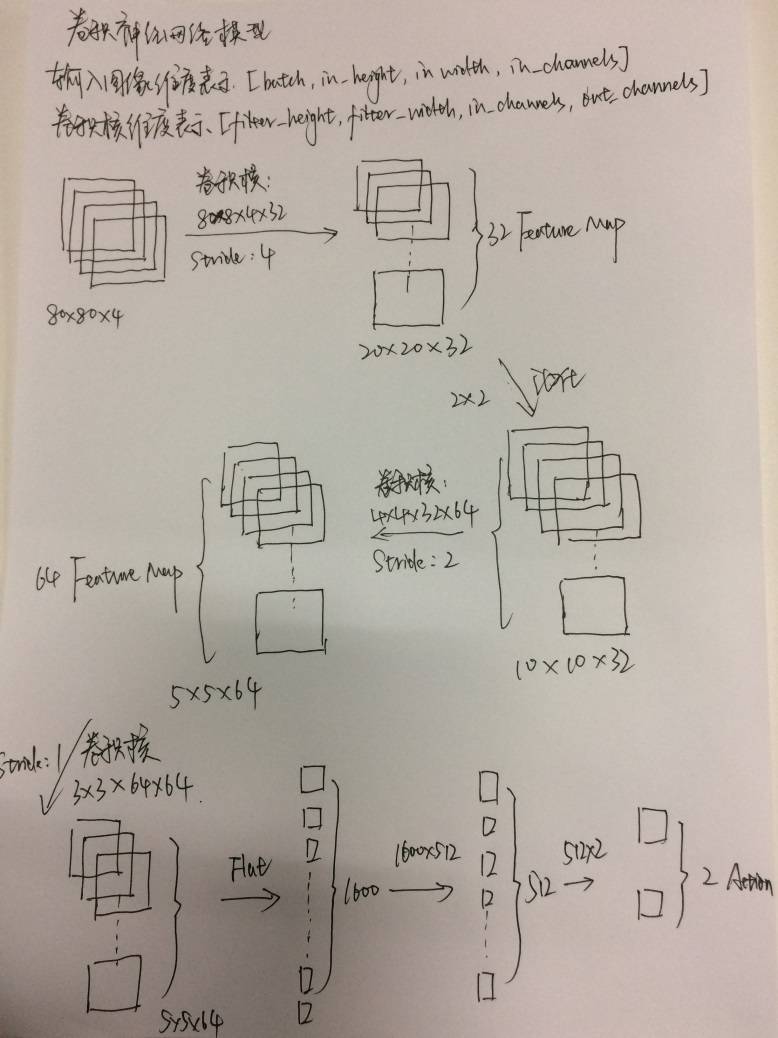
卷积神经网络模型
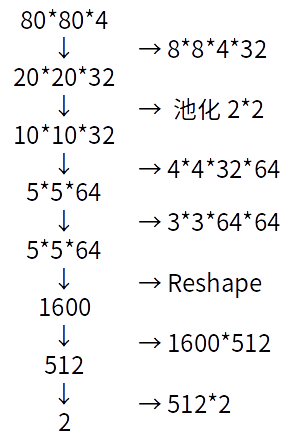
图像的处理过程
-
初始输入四幅图像80×80×4(4代表输入通道,初始时四幅图像是完全一致的),经过卷积核8×8×4×32(输入通道4,输出通道32),步距为4(每步卷积走4个像素点),得到32幅特征图(feature map),大小为20×20;
-
将20×20的图像进行池化,池化核为2×2,得到图像大小为10×10;
-
再次卷积,卷积核为4×4×32×64,步距为2,得到图像5×5×64;
-
再次卷积,卷积核为3×3×64*64,步距为2,得到图像5×5×64,虽然与上一步得到的图像规模一致,但再次卷积之后的图像信息更为抽象,也更接近全局信息;
-
Reshape,即将多维特征图转换为特征向量,得到1600维的特征向量;
-
经过全连接1600×512,得到512维特征向量;
-
再次全连接512×2,得到最终的2维向量[0,1]和[1,0],分别代表游戏屏幕上的是否点击事件。
可以看出,该模型实现了端到端的学习,输入的是游戏屏幕的截图信息(代码中经过opencv处理),输出的是游戏的动作,即是否点击屏幕。深度学习的强大在于其数据拟合能力,不需要传统机器学习中复杂的特征提取过程,而是依靠模型发现数据内部的关系。
不过这也带来另一方面的问题,那就是深度学习高度依赖大量的标签数据,而这些数据获取成本极高。
三、算法:Deep Q Network
有了卷积神经网络模型,那么怎样训练模型?使得模型收敛,从而能够指导游戏动作呢?机器学习分为监督学习、非监督学习和强化学习,这里要介绍的Q Network属于强化学习(Reinforcement Learning)的范畴。在正式介绍Q Network之前,先简单说下它的光荣历史。
2014年Google 4亿美金收购DeepMind的桥段,大家可能听说过。那么,DeepMind是如何被Google给盯上的呢?最终原因可以归咎为这篇论文:
DeepMind团队通过强化学习,完成了20多种游戏,实现了端到端的学习。其用到的算法就是Q Network。2015年,DeepMind团队在《Nature》上发表了一篇升级版:
自此,在这类游戏领域,人已经无法超过机器了。后来又有了AlphaGo,以及Master,当然,这都是后话了。其实本文也属于上述论文的范畴,只不过基于TensorFlow平台进行了实现,加入了一些笔者自己的理解而已。
回到正题,Q Network属于强化学习,那么先介绍下强化学习。
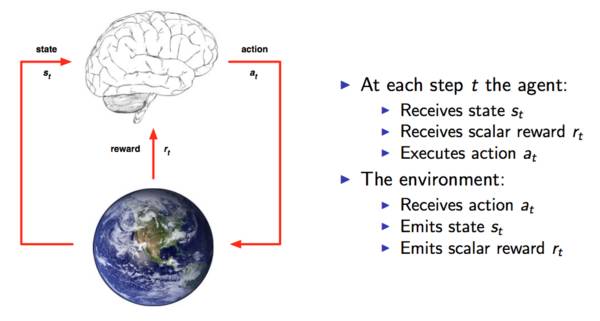
强化学习模型
强化学习过程有两个组成部分:
如图所示,在每步迭代过程中,首先智能代理(学习系统)接收环境的状态st,然后产生动作at作用于环境,环境接收动作at,并且对其进行评价,反馈给智能代理rt。不断的循环这个过程,就会产生一个状态/动作/反馈的序列:(s1, a1, r1, s2, a2, r2.....,sn, an, rn),而这个序列让我们很自然的想起了:
马尔科夫决策过程
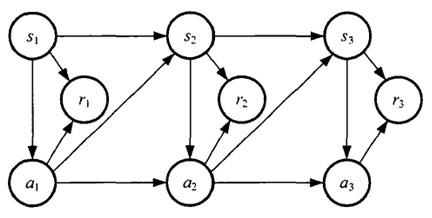
MDP:马尔科夫决策过程
马尔科夫决策过程与著名的HMM(隐马尔科夫模型)相同的是,它们都具有马尔科夫特性。那么什么是马尔科夫特性呢?简单来说,就是未来的状态只取决于当前的状态,与过去的状态无关。
HMM(马尔科夫模型)在语音识别,行为识别等机器学习领域有较为广泛的应用。条件随机场模型(Conditional Random Field)则用于自然语言处理。两大模型是语音识别、自然语言处理领域的基石。
上图可以用一个很形象的例子来说明。比如你毕业进入了一个公司,你的初始职级是T1(对应图中的 s1),你在工作上刻苦努力,追求上进(对应图中的a1),然后领导觉得你不错,准备给你升职(对应图中的r1),于是,你升到了T2;你继续刻苦努力,追求上进......不断的努力,不断的升职,最后升到了sn。当然,你也有可能不努力上进,这也是一种动作,换句话说,该动作a也属于动作集合A,然后得到的反馈r就是没有升职加薪的机会。
这里注意下,我们当然希望获取最多的升职,那么问题转换为:如何根据当前状态s(s属于状态集S),从A中选取动作a执行于环境,从而获取最多的r,即r1 + r2 ……+rn的和最大 ?这里必须要引入一个数学公式:状态值函数。
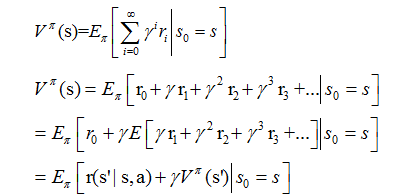
状态值函数模型
公式中有个折合因子γ,其取值范围为[0,1],当其为0时,表示只考虑当前动作对当前的影响,不考虑对后续步骤的影响,当其为1时,表示当前动作对后续每步都有均等的影响。当然,实际情况通常是当前动作对后续得分有一定的影响,但随着步数增加,其影响减小。
从公式中可以看出,状态值函数可以通过迭代的方式来求解。增强学习的目的就是求解马尔可夫决策过程(MDP)的最优策略。
策略就是如何根据环境选取动作来执行的依据。策略分为稳定的策略和不稳定的策略,稳定的策略在相同的环境下,总是会给出相同的动作,不稳定的策略则反之,这里我们主要讨论稳定的策略。
求解上述状态函数需要采用动态规划的方法,而具体到公式,不得不提:
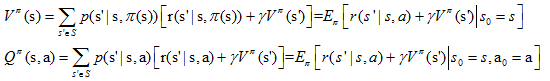
贝尔曼方程
其中,π代表上述提到的策略,Q π (s, a)相比于V π (s),引入了动作,被称作动作值函数。对贝尔曼方程求最优解,就得到了贝尔曼最优性方程。
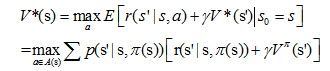
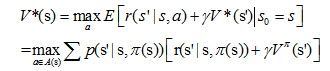
状态值函数最优解
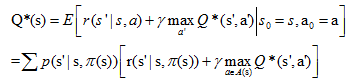
动作值函数最优解
求解该方程有两种方法:策略迭代和值迭代。
策略迭代分为两个步骤:策略评估和策略改进,即首先评估策略,得到状态值函数,其次,改进策略,如果新的策略比之前好,就替代老的策略。





