正文
回到主题,AC 模型有两个恰如其分的名字:行为和评判。前者接受当前的环境状态,并决定从哪个状态获得最佳动作。它以非常类似于人类自身的行为方式来实现 DQN 算法。评判模块通过从 DQN 中接受环境状态和动作并返回一个表征动作状态的分数来完成评判功能。
把这想象成是一个孩子(「行为模块」)与其父母(「评判模块」)的游乐场。孩子正在环顾四周,探索周边环境中的所有可能选择,例如滑动幻灯片,荡秋千,在草地上玩耍。父母会照看孩子并基于其所为,对孩子给出批评或补充。父母的决定依赖于环境的事实无可否认:毕竟,如果孩子试图在真实的秋千上玩耍,相比于试图在幻灯片上这样做,孩子更值得表扬!
简介:链式法则(可选)
你需要理解的主要理论在很大程度上支撑着现代机器学习:链式法则。毫不夸张的说链式法则可能是掌握理解实用机器学习的最关键的(即使有些简单)的想法之一。事实上,如果只是直观地了解链式法则的概念,你并不需要很深厚的数学背景。我会非常快速地讲解链式法则,但如果你已了解,请随意跳到下一部分,下一部分我们将看到开发 AC 模型的实际概述,以及链条法则如何适用于该规划。

一个看似可能来自你第一节微积分课堂上的简单概念,构成了实用机器学习的现代基础,因为它在反向推算和类似算法中有着令人难以置信的加速运算效果。
这个等式看起来非常直观:毕竟只是「重写了分子/分母」。这个「直观的解释」有一个主要问题:等式中的推导完全是倒退的!关键是要记住,数学中引入直观的符号是为了帮助我们理解概念。因此,由于链式法则的计算方式非常类似于简化分数的运算过程,人们才引入这种「分数」符号。那么试图通过符号来解释概念的人正在跳过关键的一步:为什么这些符号可以通用?如同这里,为什么要像这样进行求导?
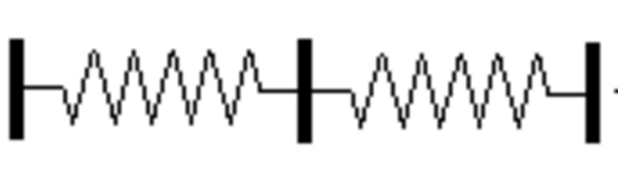
可以借助经典的弹簧实例可视化运动中的链条规则
基本概念实际上并不比这个符号更难理解。想象一下,我们把一捆绳子一根根地系在一起,类似于把一堆弹簧串联起来。假设你固定了这个弹簧系统的一端,你的目标是以 10 英尺/秒的速度摇晃另一端,那么你可以用这个速度摇动你的末端,并把它传播到另一端。或者你可以连接一些中间系统,以较低的速率摇动中间连接,例如,5 英尺/秒。也就是说,在 5 英尺/秒的情况下,你只需要以 2 英尺/秒的速度摇动末端,因为你从开始到终点做的任何运动都会被传递到终点位置。这是因为物理连接迫使一端的运动被传递到末端。注意:和其它类比一样,这里有一些不当之处,但这主要是为了可视化。
类似地,如果我们有两个系统,其中一个系统的输出是另一个系统的输入,微调「反馈网络」的参数将会影响其输出,该输出会被传播下去并乘以任何进一步的变化值并贯穿整个网络。
AC 模型概述
因此,我们必须制定一个 ActorCritic 类,它包含一些之前实现过的 DQN,但是其训练过程更复杂。因为我们需要一些更高级的功能,我们必须使用包含了基础库 Keras 的开源框架:Tensorflow。注意:你也可以在 Theano 中实现这一点,但是我以前没有使用过它,所以没有包含其代码。如果你选择这么做,请随时向 Theano 提交此代码的扩展。
模型实现包含四个主要部分,其直接并行如何实现 DQN 代理:
AC 参数
第一步,导入需要的库
import gym
import numpy as np
from keras.models import Sequential, Model
from keras.layers import Dense, Dropout, Input
from keras.layers.merge import Add, Multiply
from keras.optimizers import Adam
import keras.backend as K
import tensorflow as tf
import random
from collections import deque
参数与 DQN 中的参数非常类似。毕竟,这个行为-评判模型除了两个独立的模块之外,还要做与 DQN 相同的任务。我们还继续使用我们在 DQN 报告中讨论的「目标网络攻击」,以确保网络成功收敛。唯一的新参数是「tau」,并且涉及在这种情况下如何进行目标网络学习的细微变化:
class ActorCritic:
def __init__(self, env, sess):
self.env = env
self.sess = sess
self.learning_rate = 0.001
self.epsilon = 1.0
self.epsilon_decay = .995
self.gamma = .95
self.tau = .125
self.memory = deque(maxlen=2000)















