一文读懂递归算法

算法爱好者 · 公众号 · 算法 · 2017-12-19 08:25

正文

请到「今天看啥」查看全文

，则过程如下：

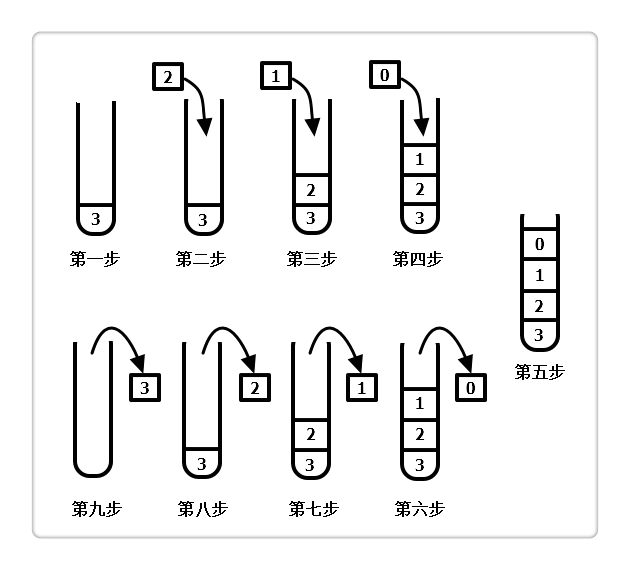
第 1~4 步，都是入栈过程， Factorial(3) 调用了 Factorial(2) ， Factorial(2) 又接着调用 Factorial(1) ，直到 Factorial(0) ；
第 5 步，因 0 是递归结束条件，故不再入栈，此时栈高度为 4，即为我们平时所说的递归深度；
第 6~9 步， Factorial(0) 做完，出栈，而 Factorial(0) 做完意味着 Factorial(1) 也做完，同样进行出栈，重复下去，直到所有的都出栈完毕，递归结束。

每一个递归程序都可以把它改写为非递归版本。 我们只需利用栈，通过入栈和出栈两个操作就可以模拟递归的过程，二叉树的遍历无疑是这方面的代表。

但是并不是每个递归程序都是那么容易被改写为非递归的。某些递归程序比较复杂，其入栈和出栈非常繁琐，给编码带来了很大难度，而且易读性极差，所以条件允许的情况下，推荐使用递归。

三：如何思考递归

在初学递归的时候, 看到一个递归实现, 我们总是难免陷入不停的验证之中，比如上面提及的阶乘，求解 Factorial(n) 时，我们总会情不自禁的发问， Factorial(n-1) 可以求出正确的答案么？接着我们就会再用 Factorial(n-2) 去验证，，，不停地往下验证直到 Factorial(0) 。

对递归这样的不适应，和我们平时习惯的思维方式有关。我们习惯的思维是：已知 Factorial(0) ，乘上 1 就等于 Factorial(1) ，再乘以 2 就等于 Factorial(2) ，，，直到乘到 n。

而递归和我们的思维方式正好相反。

那我们怎么判断这个递归计算是否是正确的呢？Paul Graham 提到一种方法，如下：

如果下面这两点是成立的，我们就知道这个递归对于所有的 n 都是正确的。

当 $n = 0, 1 " role="presentation" style="box-sizing: border-box; outline: 0px; display: inline-block; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border-width: 0px; border-style: initial; border-color: initial;">$ 时，结果正确；

假设递归对于 $n " role="presentation" style="box-sizing: border-box; outline: 0px; display: inline-block; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border-width: 0px; border-style: initial; border-color: initial;">$ 是正确的，同时对于 $n + 1 " role="presentation" style="box-sizing: border-box; outline: 0px; display: inline-block; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border-width: 0px; border-style: initial; border-color: initial;">$ 也正确。