正文
基于定理5.7,可以得到一个动态规划(DP)算法。考虑 q 中的一个子问题 qi 是 (1) 一个初始 BFQ(不可分解)或(2)一个可被进一步分解的问题串中的其中一个。对于情形(1),A*(qi) 包括一个元素也就是 qi 本身。对于情形(2),A *(qi) = A *(qj) ⊕r(qi,qj),其中 qj ⊂qi 有最大 P(r(qi,qj))P(A *(qj)),r(qi,qj) 是通过将 qi 中的 qj 用一个占位符“$e”替换而生成的问题。从而得到动态规划方程:
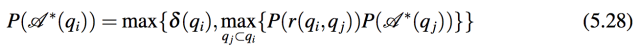
其中 δ(qi) 是决定 q1 是否为初始 BFQ 的指示函数。也就是说,当 qi 是初始 BFQ 或 δ(qi) =0 时,δ(qi)=1。
算法 2 描述了动态规划算法。算法在外层循环(第 1 行)中枚举 q 的所有子串。在每个循环中,算法首先初始化 A *(qi)和P(A *(qi))(第 2-4 行)。在内层循环中,算法枚举 qi 的所有子串 qj(第 5 行),然后更新 A *(qi) 与 P(A *(qi))(第 7-9 行)。注意到算法按照长度升序枚举所有 qi,这确保了通过每个被枚举的 qj,可以知道它们的 P(A *()) 和 A *()。
因为每个循环枚举 O(|q|2) 个子串,从而算法 2 的复杂度为 O(|q|4)。在实验的 QA 语料库中,超过 99% 的问题字数少于 23 个 (|q| < 23),因此这样的复杂度是可以接受的。

第 6 节 属性扩展
在知识图谱中,许多关系不是由一个直接属性表达的,而是由一条由许多属性组成的路径表示的。正如图 1.1 所示,在 RDF 数据库中,“spouse of”关系是由三个属性 marriage → person → name 表达的。本章称这些多属性的路径为扩展属性。利用扩展属性来回答问题可以高效提升 KBQA 的覆盖率。
定义 5.8
(扩展属性)一个扩展属性 p+ 是一个属性序列 p+ = (p1,..., pk)。本章把 k 称为 p+ 的长度。如果存在一个宾语序列 s = (s1,s2,...,sk) 使得 ∀1 ≤ i < k,(si, pi,si+1) ∈ K 且 (sk, pk,o) ∈ K ,则说 p+ 连接了主语 s 和宾语 o。正如 (s, p,o) ∈ K 表示了 p 连接了 s 和 o,这里将 p+ 连接 s 和 o 记作 (s, p+,o) ∈ K 。
第3节中提出的KBQA模型可以充分适应属性拓的问题。系统只需要一些轻微的调整就可以使得KBQA对扩展属性有效。第6.1.节展示了这种调整。第6.2.节展示了如何 使得它对十亿级别的数据库有效。最后,第6.3.节中展示了如何选择一个合理的属性长度来保证最高的效率。
6.1. 对扩展属性的 KBQA
上文曾提到,对单一属性的 KBQA 由两大部分组成。在离线部分,系统计算对给定模板的属性分布 P(p|t);在线上部分,系统抽取问题的模板 t,然后通过 P(p|t) 计算它的属性。当把 p 替换成 p+ 之后,系统做了如下调整:
在
离线
部分,系统学习了对扩展属性的问题模板。例如计算 P(p+|t)。 P(p+|t) 的计算仅仅只要知道 (e, p+ , v) 是否在 K 中。如果系统生成了所有的 (e, p+ , v) ∈ K ,就可以计算这一存在性。第 6.2. 节展示了这一生成过程。
在
线上
部分,系统用扩展属性来回答问题。系统可以通过 RDF 数据库中的 e 到 p+ 来计算 P(v|e, p+)。例如,让 p+ = marriage → person → name,为了从图 1.1 中的数据库来计算 P(v|Barack Obama, p+),系统从节点 a 开始遍历,然后经过节点 b 和 c,最后得到了 P(Michelle Obama|Barack Obama, p+) = 1。
6.2. 扩展属性的生成
一个简单的生成所有的扩展属性的方式是对数据库中的每一个节点进行广度优先搜索(BFS)。然而,扩展属性的数量随着属性的长度指数级增长。所以当数据量达到十亿级别的时候,BFS 的开销是无法承受的。
为了实现扩展属性的生成,系统首先对属性的长度 k 设置了限制来提升延展性,也就是说,它只搜索长度小于等于 k 的扩展属性。下一个小节会展示如何得到一个合适的 k。本节通过另外两个方面来提升延展性:(1) s 的约减;(2) 内存高效的 BFS。
s 的约减:
离线处理的过程只对在 QA 语料库中出现过至少一次的 s 有兴趣。因此,系统只用那些在 QA 语料库中的问题中出现过的宾语作为 BFS 的起始节点。这一策略很大程度上减少了生成的 (s, p+ , o) 的数量,因为这些实体的数量比起在十亿级别数据库中的要少得多。在系统使用的数据库(15 亿实体)和 QA 语料库(79 万不同实体)中,这一过滤策略理论上可以减少 (s, p+ , o) 的数量 1500/0.79 = 1899 倍。
内存高效的 BFS:
为了在 1.1TB 大小的数据库中使用 BFS,本节使用了基于磁盘的多源 BFS 算法。在一开始,系统将在 QA 语料库(记作 S0)中出现过的所有的实体读取入内存,并在 S0 创建了一个散列索引。第一轮中,系统通过扫描磁盘上的所有 RDF 三元组一次,并将三元组的主语和 S0 结合,我们就得到了所有长度为 1 的 (s, p+,o)。本节建立的对 S0 的散列索引,允许算法在线性时间内完成这一操作。第二轮中,系统将所有的三元组读入进内存中,然后建立对所有的宾语 o 建立散列索引(记作 S1)。然后再次扫描 RDF,并将 RDF 中三元组的主语和 s ∈ S1 结合。现在系统得到所有的长度为 2 的 (s, p+,o),并将它们读入进内存中。系统重复上述的“索引+扫描+结合”操作 k 次来得到所有的长度为 p+.length ≤ k 的 (s, p+,o)。
这个算法非常高效,其时间消耗主要用在了 k 次扫描数据库上。散列索引的建立和结合的操作在内存中执行,时间消耗对于磁盘上的 I/O 来说是可以忽略不计的。注意到从 S0 开始的扩展属性的数量总是比数据库的大小要小得多,因此可以被容纳在内存中。对于实验使用的数据库(KBA,更多细节请参阅实验章节)和 QA 语料库,只需要存储 21M 的 (s, p+,o) 三元组。所以很容易将他们读入内存。假设 K 的大小是 |K |,算法找到的 (s, p+,o) 三元组的数量是 #spo,它消耗了 O(#spo) 的内存,算法的时间复杂度是 O(|K |+#spo)。
6.3. k 的选择
扩展属性的长度限制k影响了属性扩展的效率。k 越大,(s, p+,o) 越多,导致更高的答案覆盖率。然而,这也产生了更多的无意义的 (s, p+,o) 三元组。例如,图 1.1 中,扩展属性 marriage → person → dob 连接了“Barack Obama” 和 “1964”,但是他们明显没有关系,对于 KBQA 也没有用。
属性扩展需要选择一个能够得到最多的有意义的关系,并且排除最多无意义的关系的 k 的值。本文使用 Wikipedia 的 Infobox 估计最佳的 k。Infobox 存储了实体的一些知识,并且大部分条目都是以“主语- 属性-宾语”的三元组的形式存储的。Infobox 中的条目可以被视作有意义的关系。因此,k 的选择中首先列举一些长度为 k 的 (s, p+,o) 三元组,然后测试它们中有多少在 Infobox 中出现。选择过程希望看到 k 值的减少。
特别地,实验按照它们出现的频率的顺序,从 RDF 数据库中选择了前 17000 个实体。实体 e 出现的频率被定义为在 K 中存在的使得 e = s 的 (s, p, o) 三元组的数量。选取这些实体是因为他们有更多的知识,因此更值得信任。对于这些实体,使用第 6.2. 节中提出的 BFS 生成了他们的长度为 k 的 (s, p+,o) 三元组。然后,对于每一个 k,计算这些可以在 Wikipedia 的 Infobox 中找到对应的 (s, p+,o) 三元组的数量。更形式化地,假设 E 是作为例子的条目的集合,SPOk 是长度为 k 的 (s, p+,o) ∈ K 。定义 valid(k) 来度量 k 对于有意义的关系的数量,方法如下:





