正文
模型选择有个非常大的局限性,就是我们没有办法预先确定哪些参数相对有用,哪些无用,只有毫无规律地瞎猜。看样子这种方案不太行得通。

有没有办法能预先就判定出相对“有用”的参数呢?我们可以借鉴
数据
的降维方法,这可是数据科学家
(本文的数据科学家更关注数据的处理和分析,数理统计学家更关注参数的处理和分析,两种思维是有差别的)
的专长
。其中最为出名的方法叫做
主成分分析
(Principle component analysis)
。
什么叫高维数据呢?给定一个数据x,我们可以把这个数据看作一个向量,这个向量的每个分量都表示这个向量的某一个属性。例如“天气”,它由很多子属性构成——温度、湿度、降水量、能见度、风力、阳光强度、舒适度等等,于是这样一个简单的天气数据向量就包含了以上七个分量,是一个七维数据!就算是不了解数据分析的读者也可以看出,这个天气数据的七个分量之间存在着暧昧不清的关系,比如“湿度”必然和“降水量”有关,“舒适度”和前面几个分量都有关。那么能不能把“湿度”和“降水量”结合成一个新的分量?能不能把“舒适度”用其他分量表示?这就是数据的降维,也是主成分分析的基本思想,形成的新分量就是所谓的
主成分
。
如何把这种简单的思想翻译为精确的数学语言呢?简要地说,数学上用
矩阵X
(n×k,n是数据个数,k是数据维数,相当于把所有数据排列为一个矩阵)
来表示高维数据的集合,称为
设计矩阵
(Design Matrix)
。如果想提取数据的m个主成分,那么就通过计算矩阵X'X
(X'表示X的转置,注意X'X是一个对称矩阵)
的最大m个特征值对应的特征向量。而这m个特征向量则完全决定了前m个主成分的取法。

矩阵对角化。A若对称,那么P可以是正交阵,对角化相当于矩阵"旋转"
到此为止,数学家们已经心满意足了:“主成分嘛,不就是找对称矩阵的特征向量,用矩阵旋转的方法就可以搞定了!”但是数据科学家和计算科学家们还远不满足——实际计算中,矩阵对角化非常耗时耗力,例如要把一个k×k对称矩阵对角化,用QR分解的计算复杂度为O(k^3)[4]
(读者可自己验证)
,
在只需要很少几个主成分的情况下,这是没有必要的。于是通常的做法是先找出最大的特征值,得到相应的主成分,再按需要依次提取出更多的主成分。省时又省力,何乐而不为哉?计算复杂度是非常实际并且重要的概念,也是很多擅长理论的专家没有考虑过的因素,这也在一定程度上形成了理论界和应用界之间的鸿沟。
三、参数好坏的衡量——Fisher信息矩阵
回到对参数降维的问题。参数降维和数据降维之间是差异的——模型中的参数往往是满足限制条件的,而且和数据不一样,这些限制条件并不能直接用矩阵表示出来。这时候,熟悉数理统计的读者可能会联想到一个概念——极大似然估计中的Fisher信息矩阵
(Fisher information matrix)
,因为
Fisher信息矩阵告诉了我们每个参数的估计方差
。我们可以扔掉方差较大的参数
(因为方差大,说明这个参数对模型影响小)
,至少得缩减它们在模型中的戏份
。
我们来回顾一下极大似然估计的定义:
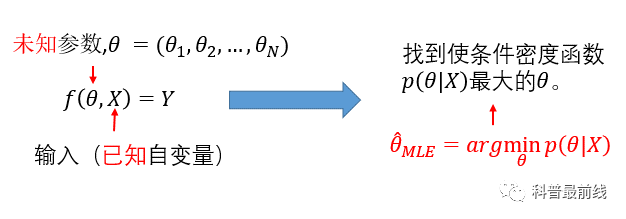
θ_MLE上面有一顶“帽子”,表示这是一个估计,一个
随机变量
,而非真实值。既然是随机变量,那么必然就有的误差,这种误差该如何衡量呢?当θ和x都是一维参数时,CR不等式
(又名CR上界)
告诉你答案:
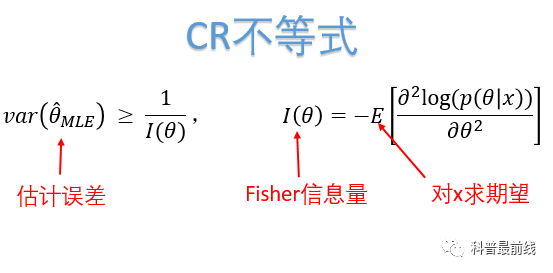
也就是说估计误差由Fisher信息量所决定。其证明思想并不复杂,主要是利用柯西不等式和概率密度函数的性质。有兴趣的读者可以参考
(这是小编四年前参加某数学竞赛面试时自创的方法,至今记忆犹新。时光荏苒,青葱岁月,现亲笔写下来,以作纪念)
:

很久不写字,丑了许多(虽然原来也不好看)
当数据x维数增大时,θ
(可以是高维参数)
的极大似然估计满足
中心极限定理
(渐进正态)
,其协方差矩阵为Fisher信息矩阵的逆。














