正文
案例共有两个自变量(两种生产原料),一个因变量(产品产量)。根据常识可知,标准化生产的产品都是固定规格的,因此原料和产量间的关系是非常明确的线性关系,但是由于生产线上残次品,生产工艺缺陷原因造成的物料损耗等必然超耗的存在,每种原料的真实使用量与产品规格内原料比例存在差异。这里的超耗可以分成两种情况,如果是由生产线不稳定引起的,那么超耗的波动是很大的,而且时高时低;如果是由工艺缺陷引起的超耗,那么这部分损耗在工艺缺陷没有改进取值会一直稳定的存在。根据以上的分析,可以先对数据进行多元线性回归分析,然后与原有规格比例对比。
线性回归分析
线性回归分析的
SPSS
操作过程已经在前面介绍过了(回顾:
数据分析技术:多重线性模型;也难也不难的建模从这里开始吧!
),这里省略操作步骤,直接解释结果。
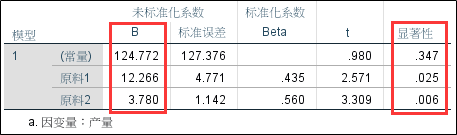
由上表的分析结果可知,两种原材料都和产品产量有线性关系,相应的二元线性回归方程为:
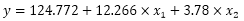
为了观察数据分布情况和回归方程的拟合情况,绘制两种原材料消耗量与产品产量之间散点图:
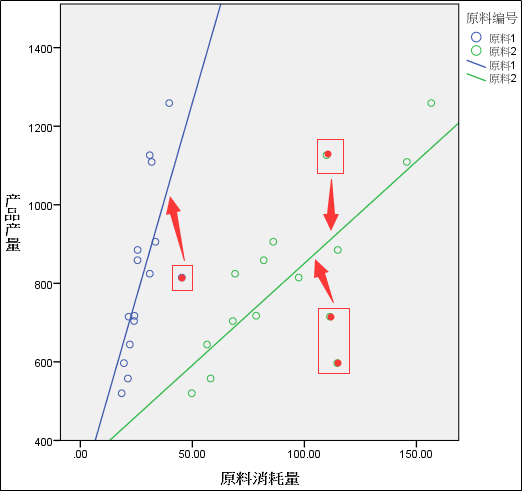
从上图可以看出,两种原料消耗量和产量间均呈较明显的线性关系,图中还分别绘制出采用最小二乘法拟合出的两个自变量回归方程的回归线。但其中原料
1
和原料
2
都存在一些数据点偏离主要趋势较远的情况出现,这也充分体现了新生产线生产过程不稳定的特点,偶尔出现生产故障导致的原料消耗过多,在回归模型中表现为强影响点(异常值)。由于后期生产会越来越稳定,在保证生产的前提下,原料的使用量受极端值的影响情况会越来越少,因此可以考虑降低极端值对回归曲线的影响力,采用最小一乘法拟合线性模型。
操作步骤
1
、选择菜单【分析】





