正文
若将成本函数定义为均方误差,则可写成:
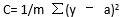
m在这里是训练输入值(training inputs),a 是预计值,y是特定事例中的实际值。
学习过程围绕着如何最小化成本。
10)
梯度下降(Gradient Descent)
–——梯度下降是一种优化算法,以最小化成本。想象一下,当你下山时,你必须一小步一小步往下走,而不是纵身一跃跳到山脚。
因此,我们要做的是:比如,我们从X点开始下降,我们下降一点点,下降ΔH,到现在的位置,也就是X-ΔH,重复这一过程,直到我们到达“山脚”。“山脚”就是最低成本点。
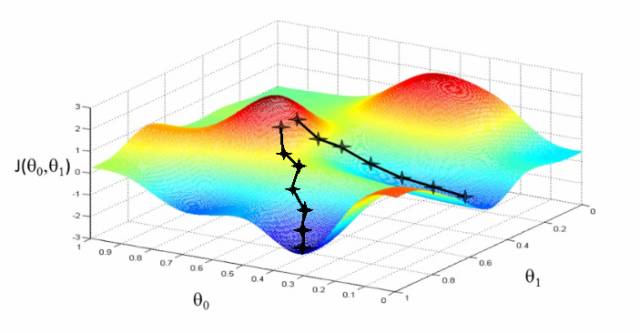
从数学的角度来说,要找到函数的局部极小值,须采取与函数梯度负相关的“步子”,即:梯度下降法是用负梯度方向为搜索方向的,梯度下降法越接近目标值,步长越小,前进越慢。
11)
学习速率 (Learning Rate)
–——学习率指每次迭代中对成本函数的最小化次数。简单来说,我们把下降到成本函数最小值的速率称为学习率。选择学习率时,我们必须非常小心,学习率既不应过大——会错过最优解,也不应过小——使网络收敛将需要很多很多步、甚至永不可能。
12)
反向传播(Back propagation)
–——在定义一个神经网络的过程中, 每个节点会被随机地分配权重和偏置。
一次迭代后,我们可以根据产生的结果计算出整个网络的偏差,然后用偏差结合成本函数的梯度,对权重因子进行相应的调整,使得下次迭代的过程中偏差变小。
这样一个结合成本函数的梯度来调整权重因子的过程就叫做反向传播。在反向传播中,信号的传递方向是朝后的,误差连同成本函数的梯度从输出层沿着隐藏层传播,同时伴随着对权重因子的调整。
13)
分批 (Batches)
—— 当我们训练一个神经网路时,我们不应一次性发送全部输入信号,而应把输入信号随机分成几个大小相同的数据块发送。
与将全部数据一次性送入网络相比,在训练时将数据分批发送,建立的模型会更具有一般性。
14)
周期 (Epochs)
—— 一个周期表示对所有的数据批次都进行了一次迭代,包括一次正向传播和一次反向传播,所以一个周期就意味着对所有的输入数据分别进行一次正向传播和反向传播。
训练网络周期的次数是可以选择的,往往周期数越高,模型的准确性就越高,但是,耗时往往就越长。同样你还需要考虑如果周期/纪元的次数过高,那么可能会出现过拟合的情况。
15)
Dropout方法
——
Dropout是一个可以阻止网络过拟合的规则化方法。就像它的名字那样,在训练过程中隐藏的某些特定神经元会被忽略掉(drop)。
这意味着网络的训练是在几个不同的结构上完成的。这种dropout的方式就像是一场合奏,多个不同结构网络的输出组合产生最终的输出结果。
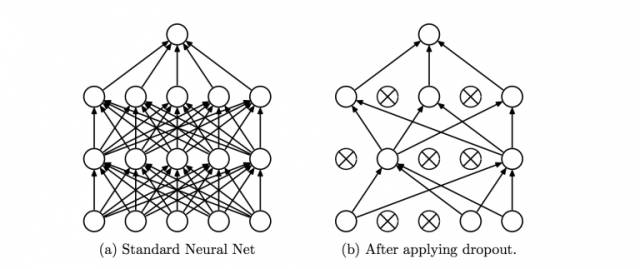
来源:
Hinton
论文《
Improving neural networks by preventing co-adaptation of featuredetectors
》
地址:
https://arxiv.org/pdf/1207.0580.pdf
16)
分批标准化 (Batch Normalization)
–——分批标准化就像是人们在河流中用以监测水位的监察站一样。
这是为了保证下一层网络得到的数据拥有合适的分布。在训练神经网络的过程中,每一次梯度下降后权重因子都会得到改变,从而会改变相应的数据结构。
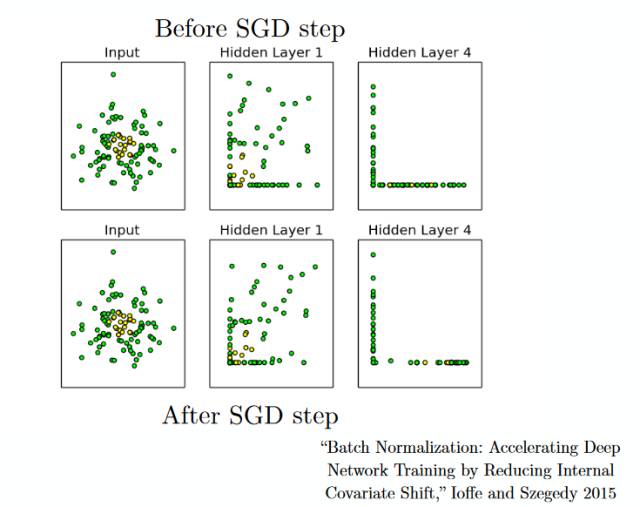
但是下一层网络希望能够得到与之前分布相似的数据,因此在每一次数据传递前都需要对数据进行一次正则化处理。






