正文
op
.
name
)
## Const
## Variable/initial_value
## Variable
## Variable/Assign
## Variable/read
我们并不想单独观察每个 op 太久,但至少观察一个来看看真实的运算。
>>> output_value = weight * input_value
现在图中有 6 个 ops,最后一个是乘法。
>>>
op
=
graph
.
get_operations
()[
-
1
]
>>>
op
.
name
## 'mul'
>>>
for
op_input
in
op
.
inputs
:
print
(
op_input
)
## Tensor("Variable/read:0", shape=(), dtype=float32)
## Tensor("Const:0", shape=(), dtype=float32)
这说明了乘法 op 的输入来源:来自图中的其它 ops。要了解整个图,按这种方法很快会使人恹恹欲睡。所以 TensorBoard graph visualization 就应运而生了。
怎样查看生成了些什么呢?我们必须“运行” output_value op。但它取决于变量:weight。我们将初始的 weight 设为 0.8,但这个值在当前会话中还没有设置。tf.initialize_all_variables() 函数会生成一个可以初始化所有变量(虽然本例中只有一个变量)的 op,下面运行这个 op。
>>>
init
=
tf
.
initialize_all_variables
()
>>>
sess
.
run
(
init
)
运行 tf.initialize_all_variables() 后会对目前存在于图中的所有变量进行初始化,所以如果添加更多变量后,会想再次使用 tf.initialize_all_variables();但原有的 init 不包括新的变量。
下面我们准备运行 output_value 的 op。
>>>
sess
.
run
(
output_value
)
## 0.80000001
回想一下 0.8 * 1.0 进行 32 位的浮点型运算很难得到 0.8;0.80000001 是最接近的数。
在 TensorBoard 观察你的图
到目前为止,简单的图已经完成了,但通过图解(diagram)能观察会更棒。用 TensorBoard 就能生成这个图解。TensorBoard 读取命名字段(name field)并将每个 op 存储在内部(和 Python 的变量名比起来很不同)。我们可以使用这些 TensorFlow 命名并转换成更符合 Python 习惯的变量名。在这使用的 tf.mul 和前面用 * 一样都是乘法,但它可以设置 op 的命名。
>>>
x
=
tf
.
constant
(
1.0
,
name
=
'input'
)
>>>
w
=
tf
.
Variable
(
0.8
,
name
=
'weight'
)
>>>
y
=
tf
.
mul
(
w
,
x
,
name
=
'output'
)
TensorBoard 由 TensorFlow 会话创建的输出目录进行观察。我们可以用 SummaryWriter 写入这个输出,如果创建图的时候我们不做任何操作,它只会写入这个图。
当我们创建 SummaryWriter 时,第一个参数是输出目录的名称,如果不存在会自动创建。
>>> summary_writer = tf.train.SummaryWriter('log_simple_graph', sess.graph)
我们现在可以在命令行启动 TensorBoard了。
$
tensorboard
--
logdir
=
log_simple
_
graph
TensorBoard 会运行一个本地的 web 应用,在 6006 端口(“6006”是“goog”的翻转)。如果你浏览 localhost:6006/#graphs,你可以看到你在 TensorFlow 图的图解,就像图 2 所示。
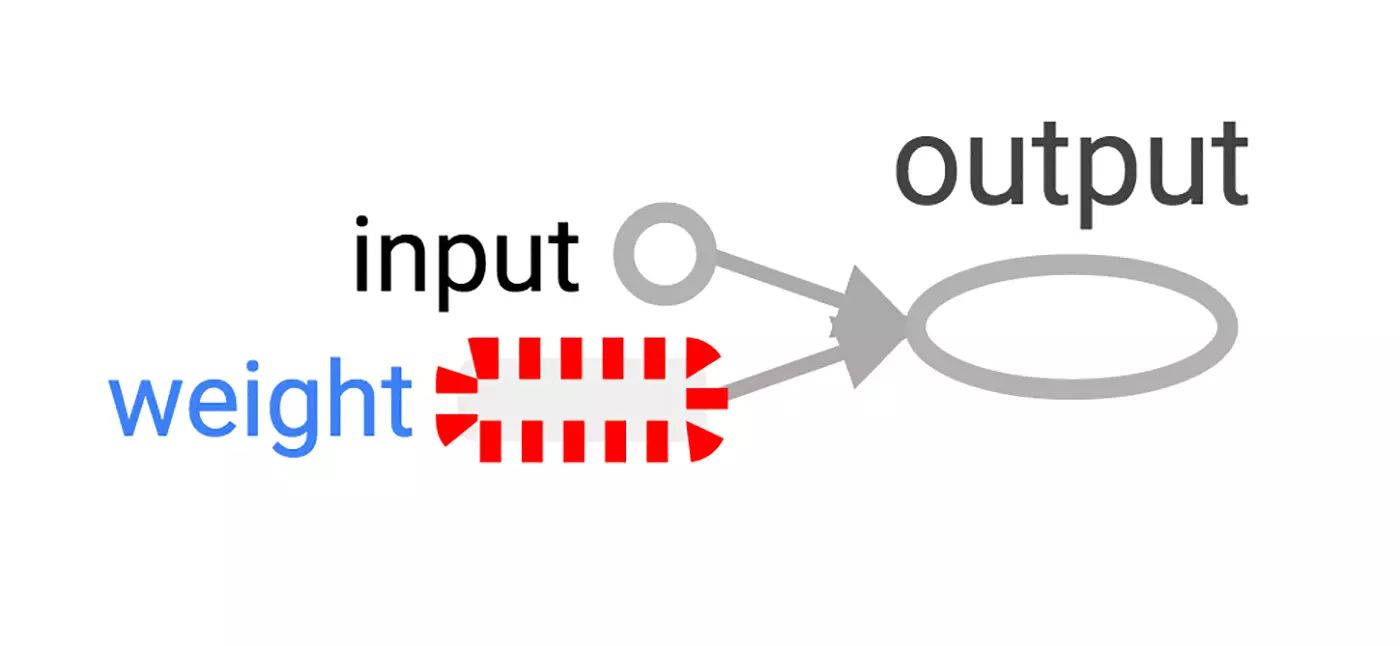
图2:最小 TensorFlow 神经元的 TensorBoard 可视化
让神经元学习
我们已经创建了神经元,但怎么让它学习呢?我们将输入值设置为 1.0,正确的输出值设置为 0。现在我们有一个非常简单的“训练集”,只有一个值为 1 的特征(feature)和值为 0 的标签(label)。我们希望这个神经元能够学会从 1 变为 0。
现在向程序输入 1,返回 0.8 的结果是不正确的。我们需要一种方式来描述系统误差。所以我们用“损失(loss)”来描述系统误差,我们的目标就是尽可能减少系统误差。当然,如果误差为负,就不是越小越好了。因此我们用实际输出(current output)和期望输出(desired output)的平方差来定义误差的值。
>>>
y_
=
tf
.
constant
(
0.0
)
>>>
loss
=
(
y
-
y_
)
**
2
目前,图里还没有东西进行学习。因此我们需要一个优化器(optimizer)。我们将使用梯度下降优化器使我们能够按照误差的导数(derivative)来更新权重。这个优化器通过学习率(learning rate)来调节(moderate)更新的大小,我们设置为 0.025。













