正文
p0.2
也小于后者得到的屈服强度R
p0.2
,两者之间相差大约1.1%。
选取表2和表3中带
∗
的试样作为代表进行分析,其对应的力-变形和力-位移曲线分别如图1和图2所示。其中力-变形曲线中的变形力F
p0.2
直接由软件读取,如图1所示,变形力F
p0.2
为39.508kN;力-位移曲线则是先将曲线图打印出来,然后在0.2mm位移处作一条与曲线弹性段平行的直线,其与曲线相交点所对应的力即为位移力F
p0.2
,结果为39.94kN。很明显变形力F
p0.2
<位移力F
p0.2
,两者之间的差距大约为1.1%,与表2和表3中的数据对比基本相符合。
表2 装夹引伸计所对应的力-变形曲线上的变形F
p0.2
和屈服强度R
p0.2

表3 不装夹引伸计所对应力-位移曲线上的位移力F
p0.2
和屈服强度R
p0.2

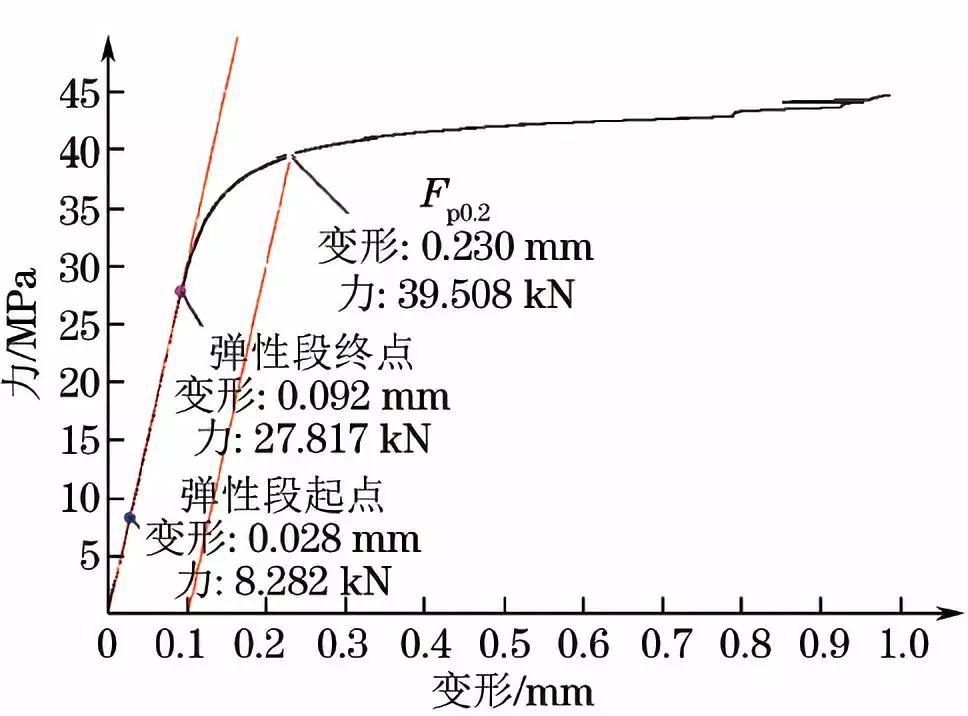
图1 装夹引伸计的力-变形曲线

图2
不装夹引伸计的力-位移曲线
继续观察力-变形与力-位移曲线,可以发现变形曲线上弹性段起点、终点所对应的力值分别为8.282kN和27.817kN,明显要先于位移曲线上的弹性段起点、终点所对应的力10.517kN 和32.492kN。由于试验机具有一定的柔度和刚度,因此,力-位移曲线上所对应的位移其实是整台设备共同的位移距离,而引伸计所探测到的变形则要比通过横梁位移所测到的更为灵敏,其探测到的是试样平行段的变形。而无论是力-变形曲线还是力-位移曲线,其本质都是通过作弹性段的平行线来测得屈服强度的数值,前者是引伸计采集的数据,而后者是仪器本身位移传感器采集的数据,因此在位移曲线上反映出来的就是平行线的斜率要小于变形曲线上的斜率,而对于无明显屈服的材料来说,试验中的力是在不断地增加的,画平行线的位移量越大得到的屈服强度越高。
2.
有明显屈服拉伸试验结果分析
表4为UnionS3NiMo1/UV420TTR合金钢焊材装夹引伸计的拉伸试验结果所对应的变形曲线上的变形力F
p0.2
和屈服强度R
p0.2
,表5为UnionS3NiMo1/UV420TTR合金钢焊材不装夹引伸计的拉伸试验结果所对应位移曲线上的位移力F
p0.2
和屈服强度R
p0.2
。对比表4和表5的结果,装夹引伸计并通过力-变形曲线读取变形力F
p0.2
的数值与不装夹引伸计并通过力-位移曲线读取位移力F
p0.2
的数值非常接近,同时前者得到的屈服强度R
p0.2
与后者得到的屈服强度R
p0.2
也相差不多。
选取表4和表5中带
∗
的试样作为代表进行分析,其对应的力-变形以及力-位移曲线分别如图3和图4所示。根据力-变形曲线变形力F
p0.2
为70.336kN,而根据力-位移曲线所作出的平行于弹性段的位移画图法的位移力F
p0.2
为70.386kN,变形力F
p0.2
与位移力F
p0.2
几乎相等。由于对明显屈服的材料来说,弹性段的直线段相对来说变化很小,即其斜率变化不大,因此尽管与无屈服材料的弹性段起点、终点情况相类似,也存在力-变形曲线上的弹性段起点、终点所对应的力值要早于力-位移曲线上的弹性段起点与终点所对应的的力值的情况,但是平行线距离对于强度取点的影响非常小,即从理论上来说位移曲线的斜率微小于变形曲线的斜率,基本可忽略不计。
表4 装夹引伸计所对应的力-变形曲线上的变形力F
p0.2
和屈服强度R
p0.2















