正文
从另一方面来看,
计算机学科的发展为现代几何提供了需求和挑战,也推动了跨学科的发展方向。
例如:
-
人工智能中的机械定理证明推动了计算代数的发展;
-
数据安全、比特币、区块链的发展推动了代数数论、椭圆曲线和模形式的发展;
-
社交网络、大数据的发展催生了持续同调理论(persistent homology)的发展;
-
动漫、游戏的发展推动了计算共性几何学科的诞生和发展;
-
机器学习的发展推动了最优传输理论的发展等等。
五、计算机&几何学研究案例
我们下面举几个具体的例子,分别是图论、计算机图形学、计算机视觉、人工智能、深度学习等。这几个和几何都有密切的联系。
1、图论
我们先讲讲图论。图,就是一大堆顶点、一大堆边把它们连起来,这是最简单不过的事情。对于一个图,譬如交通图,我们要找出它们有着怎么样一个结构,什么地方比较拥挤。有时候我们也要研究怎么将这个图切成小部分,然后分解成简单的子图;如何衡量各个连通分支间的连接度;如何将图染色等。这些问题实际上都跟图上的特征函数有密切的关系。
图上的特征函数跟光滑图形上的特征函数有很类似的地方。
我在40年前跟几个朋友,郑绍远、李伟光,做了一个工作,将光滑黎曼流形的特征函数推广到图上,得到了很好的结果。这些结果可以用来决定图上的连结的生成,研究图上的边创造过程,尤其是有个量的估值来控制在图上发散的过程。约束发散的过程可以应用到许多实际的过程中。我们还研究了图上的薛定谔方程,定义了图上的量子隧道概念。这些概念都是从物理上来的,被借用到图上。
假如我们在考虑有向图,就是每个点、每个边,给它一个方向,
我们就可以将拓扑学整个引用到图上去,定义了图上的同调群。
同调群可以用来研究图上密切的关系和它的内容。
现在我们来讲讲我们做的关于博弈理论的一个事情。进化图论为表达种群结构提供了数学工具:顶点代表个体,边代表个体的交互作用。图可以用来代表各种具有空间结构的群,例如细菌、动植物、组织结构、多细胞器官和社交网络。在进化过程中,每个个体依据自身的适应程度,进行繁殖病侵占到邻近顶点。图的拓扑反映了基因的演化——变异和选择的平衡。类似的,
互联网是一个大网,一个非常复杂的网络,我可以在上面研究它的变化。社交行为的进化可以用进化博弈论来研究。
个体和邻居博弈,根据收益而繁殖。个体繁殖速率受到自身与其他个体的交互作用影响,从而产生博弈的动态演化。其中心的问题就在于对于给定的图如何决定哪种策略会取得成功。
我们在今年年初的时候在nature上发了篇文章,我们得到一个结果,就是在任何给定的图上进行弱选择,自然选择从两种彼此竞争的策略中如何进行挑选,这个理论框架适用于人类决策,也适用于任何集群组织的生态演化。
我们从弱选择极限得到的结果,解释了何种组织结构导致何种行为。我们发现,如果存在成对的强纽带结构,合作就会大规模出现。我们用数学证明了社会学方面的一个结论:稳定的伙伴或者伴侣,对于形成合作型的社会起到了骨干作用。
2、计算机图形学:全局参数化 – 共形几何
下面我要讲的是“计算机图形学:全局参数化 – 共形几何”。这是我们发展了二十多年的一个学问。我和顾险峰从他还在哈佛念博士的时候(1999年)我们就开始做这个事情。
当我们将图形整体光滑映射到参数区域,使几何变得很小,会破坏掉整个图形;一般来讲这个要用手工来做,否则的话它变化非常大。针对这个问题,我们使用了纹理贴图、法向量贴图等等的方法。共性几何是一个很重要的从很古典的黎曼几何中产生的几何。

举例来讲,这个大卫的雕像,我们将它保角地映射到平面上去。它表面上看好像变化很大,但实际上变化不大,因为它是保角不变的。这在图像处理中是一个很重要的事情。举个例子来讲,从图上要画格点,因为我们画到平面上去以后,我们就可以将平面上画的很好的格点映射到脸上,就可以变成很漂亮的四方形的格点。这对工程处理有很多好处,
其好处就是它将图上很小的圆映射到对方图上还是一个很小的圆,不会有扭曲,不会有太大的变化。
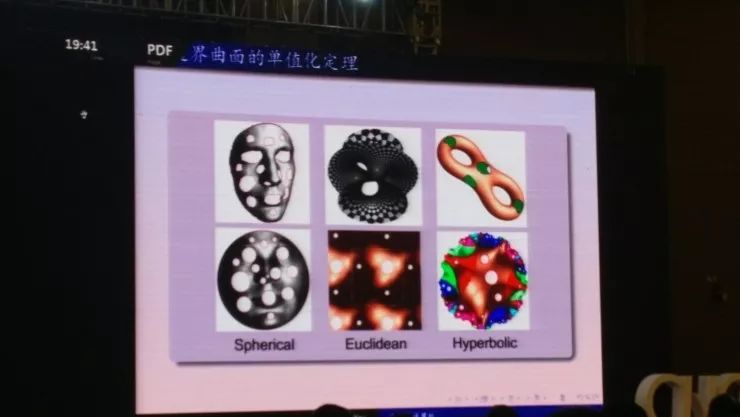
前面这些应用到一个数学上很重的定理,叫做庞加莱单值化定理,这是一个从黎曼时候开始的定理。就是讲映射的图形只跟它的拓扑性有关,这上面有三种几何,分别为:球面几何、欧氏几何、双曲几何。所有二维的几何,不管是什么样子的,我们都可以用这三种几何来分类。因此我们就可以将很复杂的事情很简单地描述出来。

上面这些我们得出了很好的结果。但是保角也有它的缺点,所以我们也发展了第二类映射,我们使得面元被保持,而角度不一定被保持。保角映射有时候可能将一个面拉的很远,左手边是保角映射,右手边是保面元映射。右面的图在不同的情形下会得出很好的结果。
3、计算机视觉,表情追踪 – 拟共映射
















