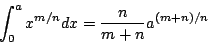和分 (summation) 探究数列的求和
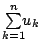 问题,积分探求函数图形在
[
a
,
b
]
之上所围成的面积,见下图 2。两者具有密切的关系。
问题,积分探求函数图形在
[
a
,
b
]
之上所围成的面积,见下图 2。两者具有密切的关系。
|
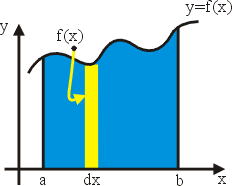
图2
|
首先观察到,和分可以解释为下面图 3 之柱状图的面积。
|
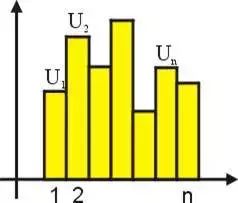
图3
|
其次将函数
y
=
f
(
x
)
离散化:作区间
[
a
,
b
]
的分割
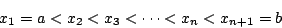
考虑和分
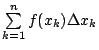 ,其几何意义就是下图 4 诸矩形所成的阴影面积,它是图 2 的近似面积。
,其几何意义就是下图 4 诸矩形所成的阴影面积,它是图 2 的近似面积。
|
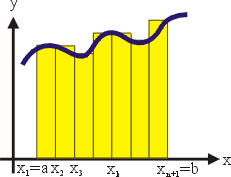
图4
|
现在想象将
[
a
,
b
]
分割成无穷多段的无穷小段
dx
(即微分),想成是差分
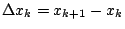 的极致(参见图 2),然后考虑无穷小矩形的面积
的极致(参见图 2),然后考虑无穷小矩形的面积
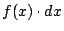 ,从
x
=
a
连续地累积到
x
=
b
。这样的求和跟和分有关但却不同,为了区别起见 Leibniz 在1686年首度将记号
,从
x
=
a
连续地累积到
x
=
b
。这样的求和跟和分有关但却不同,为了区别起见 Leibniz 在1686年首度将记号
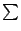 改为
改为
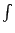 。理由是:S 表示求和 Sum 的第一个字母,将 S 稍微拉伸变成
。理由是:S 表示求和 Sum 的第一个字母,将 S 稍微拉伸变成
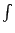 ,表示连续地求和。因此,就用美妙的记号
,表示连续地求和。因此,就用美妙的记号
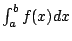 来表示图 2 阴影领域的面积,说成
f
在
[
a
,
b
]
上的积分。换言之,阴影领域的面积就是无穷多个无穷小矩形面积的连续求和,即定积分 (definite integral)。
来表示图 2 阴影领域的面积,说成
f
在
[
a
,
b
]
上的积分。换言之,阴影领域的面积就是无穷多个无穷小矩形面积的连续求和,即定积分 (definite integral)。
Leibniz
进一步把积分
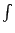 看作是微分
d
的逆运算,例如由公式
看作是微分
d
的逆运算,例如由公式
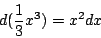
就得到
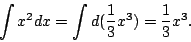
一般而言,
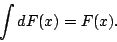
Leibniz
说:
像乘方与开方,和分与差分,
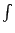 与
d
是互逆的。
与
d
是互逆的。
六.
从差和分根本定理到微积分根本定理
如何求算积分
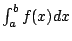 呢?
呢?
这是一个千古大难题。Archimedes 利用穷尽法 (the method of exhaustion),只会算出
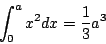
Cavalieri
(1598~1647)利用不可分割法或无穷小法 (the method of indivisible and infinitesimal) 求得
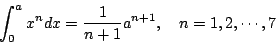
Fermat
(1601~1665)利用动态穷尽法求得