正文
36
3636=
56
36
36=
16
36=76
,
所以我们说
36
的阶是
5
,依次类推。你能算出其它成员的阶分别是几吗?
|
4
|
16
|
24
|
36
|
44
|
56
|
64
|
76
|
84
|
96
|
|
4
|
|
|
|
|
|
|
|
|
|
|
|
16
|
|
|
|
|
|
|
|
|
|
|
|
24
|
|
|
|
|
|
|
|
|
|
|
|
36
|
|
|
|
|
|
|
|
|
|
|
|
44
|
|
|
|
|
|
|
|
|
|
|
|
56
|
|
|
|
|
|
|
|
|
|
|
|
64
|
|
|
|
|
|
|
|
|
|
|
|
76
|
|
|
|
|
|
|
|
|
|
|
|
84
|
|
|
|
|
|
|
|
|
|
|
|
96
|
|
|
|
|
|
|
|
|
|
|
如果你想亲自体验到其中滋味,我建议你自己去编造一个特殊乘法表或利用下面的“乘法表”来验证第③和第④条,第①、②、⑤条要单独计算验证,对于小学生来说用笔算感觉会更加好,如果你笔算非常熟练,也可以直接用计算器算。
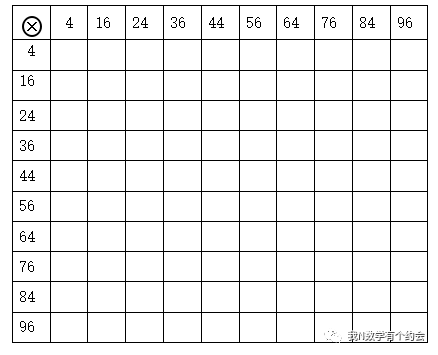
这个群其实只是我发现的群的一个子群,因为元素个数比较适中,所以我就把它放在前面了,而我最开始发现的群是由20个成员的:{4、8、12、16、24、28、32、36、44、48、52、56、64、68、72、76、84、88、92、96}
下面我将简单介绍一下,这个“独立王国”的发现过程:
之前就有耳闻:教小学生群论是可能的。我当时的感觉是:这么抽象的内容,数学专业生都不易理解,如果硬是想办法嚼碎了喂给小学生吃,意义不大。去年寒假,在家休息时,一直在看谈详柏老先生的著作《数学不了情》,从中了解到,如果定义一种
‘
截取尾数乘法
’
的话,我们就能够得到一个
8
阶五位数乘群,这个群
G=
{
46875
、
96875
、
21875
、
71875
、
90625
、
40625
、
15625
、
65625
}
,定义的乘法为
:先按普通乘法算乘积,再
截取结果末五位作为群乘的结果
。神奇的是这样的乘法对于集合
G
是封闭的,①
G
中任意两个元素按这样的乘法相乘,其结果依然还是
G
中元素,跑不出
G
的范围。②
96265
相当于
G
中的单位元;③对于
G
中每个元素,都能通过计算找到其逆元素。同时还满足交换律,所以
G
不仅是一个群,还是一个阿贝尔群。但是,由于当时没有太多感觉,就搁浅了,没有深入研究。直到今年四月中旬,开通了自己的数学公众号,准备为提高学生的数学学习兴趣和数学研究能力,分享一些资源和自己的思考。要开始着手找素材了,所以就形成了一个习题库,从中发现并改造出,对于学生全面地理解加减乘除这四种运算的题目,但同时也没有落下坚持翻看大学专业数学书籍的习惯,其中《近世代数》从毕业以来,已经翻看了两三遍,但也一直是限于自己对大学知识的复习。直到最近要找数学题素材,再次翻到了谈老的《数学不了情》,又一次看到了
{
46875
、
96875
、
21875
、
71875
、
90625
、
40625
、
15625
、
65625
}
,于是才产生要不要呈现给学生的想法,但是细想,这里面的数太大,对于三年级学生不太合适,虽然四年级学生可以用计算器来算,但我感觉这没有亲自动笔感受深刻,对于群的魅力感受也会打折扣,于是又放弃了。稍后,躺在床上,突然一个念头崩出来:五位数乘五位数太大,何不构造一个三年级就可以操作的两位数乘两位数,这个点子,马上让自己大脑兴奋起来,于是马上开灯,翻开近世代数,群论那一章,又把群的定义认真复习了一遍,接着随手在草稿纸上写了几个两位数,试着乘一下,看结果末两位有没有规律,结果感受到的是,两位数太多,无从下手
……
第二天,上完课,坐在办公室,由于暂时地闲下来了,就想起了,昨晚构造群的事情,因为想到:如果能构造出一个两位数乘两位数
‘
乘群
’
,不仅可以让学生很好地练习刚学的笔算乘法,还能让他们感受一下,群的代数结构的魔力,为他们日后学习数学专业也埋下了一颗种子,于是马上拿起纸和笔,陷入了思考:①两位数乘以两位数,结果是三或四位数,而谈老的五位数
‘
乘
’
群中的元素都是较大的五位数,如果存在两位数














