基本粒子和相互作用的标准模型 | 众妙之门​

正文

请到「今天看啥」查看全文

观测表明，通过一个大质量的物体附近的光确实被引力拉向那个物体。这是广义相对论的重要验证之一。这种性质现在已经被人们用来发现宇宙中的暗物质。实际上，依据广义相对论，物质产生引力。光携带能量，因此必然受到引力的影响。爱因斯坦认为，引力波可以从加速物体发射出来，就像加速电荷发射电磁波一样。这种现象已经在双脉冲星中看到，它的轨道由于引力波发射而失去能量而衰变。在2016年，LIGO实验室也探测到地球因引力波产生的伸缩效应。引力波的探测可以说是近些年来物理学最重大进展之一。2017年的诺贝尔物理学奖授予了对探测引力波作出重要贡献的雷纳·韦斯、巴里·巴里什和基普·S.索恩三人。在那之后2017年8月17日，LIGO和Virgo探测器又分别探测到了一个持续时间为100s左右的新引力波信号。在该引力波信号到达后大约1.7s，美国国家航空航天局 (NASA) 费米卫星搭载的伽玛暴监测器 (GBM) 、欧洲INTEGRAL和中国紫金山天文台等世界各地的多家天文台都探测到了一个暗弱的短时标电磁伽马射线暴。2017年10月16日多国天文学家同时宣布了这一消息，引起了世界的轰动，这也标志着以多种观测方式为特点的“多信使”天文学进入一个新时代 ^{[15 ]} 。

（2） 电磁相互作用

下面讨论电磁相互作用。电和磁相互作用最初被认为是互不相关的，但后来的实验表明，它们密切相连。这种联系最终由麦克斯韦在1873年提出麦克斯韦方程组来描述。与万有引力一样，静电力也遵循一个平方反比律，叫做库仑定律。不同的是，力的大小不是与两个物体的质量成正比，而是与它们电荷的乘积成正比。由于电荷既可以是正电荷，也可以是负电荷，所以电场力可以是引力 (在相反的电荷之间) ，也可以是斥力 (在同一符号的电荷之间) 。相反，质量总是正的，万有引力总是吸引力。反引力是不存在的，所谓的反粒子的质量也是正的。正是这种静电力的双极特性使得万有引力才得以被发现。由于这个特性，中性物体之间没有电。这是因为物体上带正电的部分被物体上带负电的部分上的电力抵消。如果不如此，行星和太阳之间更强的电力就会完全掩盖万有引力的效应。

电磁作用是产生光、无线电波，它还负责电子设备的运作。它是把电子和原子核结合在一起形成一个原子，再把原子结合在一起形成一个分子，把分子或原子结合在一起形成液体或固体的力。当这些原子和分子的存在使其变得复杂时，它就可以被看作是基本相互作用。在宏观层次，电磁相互作用产生了一根绳子的弹性力，或者强力胶水的粘着力，两个相互接触物体的摩擦力，液体的表面张力等等。简言之，除了重力之外，电磁力是我们在日常生活中遇到的唯一力量。

（3） 弱相互作用

剩下的两种基本相互作用是在20世纪被发现的。它们是强相互作用和弱相互作用。在日常生活中人类个体是无法体验到这两种相互作用的，因为力程非常短。两个核子之间的强相互作用力只有在它们相距10 -15 m以内时才有效 ^{[16 ]} ；弱力力程更短：约10 -17 ～10 -18 m。太阳发光发热就是因为其内部发生的核聚变反应释放的能量。核电站、原子弹及氢弹就是人类可以利用核能的例子。

弱力是造成中子不稳定的主要原因。在这个力的影响下，一个孤立的中子在大约15分钟内被分裂成一个质子、一个电子、一个反电子中微子(n→p+ 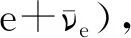这个过程被称为β衰变 ^{[17 ]} 。在强力或电磁力的影响下，有些强子也会变得不稳定，但它们的寿命通常比中子寿命小很多数量级。这正表明，与强和电磁相互作用力相比，负责β衰变的相互作用强度是弱的，因此被称为“弱相互作用”。

原子核中的中子受到强和电磁相互作用的保护，适量中子可能会保持稳定。但是如果中子数目过多，那么这种保护将不足以使它们都保持安全，原子核就产生放射性β衰变。在一些夜光表中，发光材料就是由产生放射性β衰变的物质制成的。由于β衰变，核内的中子变成质子，而产生的电子和反电子中微子离开原子核。新的原子核比旧原子核多出一个质子，不久它就会捕获一个电子来中和它。由于一种元素的化学性质是由电子或质子的数量决定的，经历β衰变的化学元素转变为另一种化学元素。再加上一个质子，额外的静电斥力会使新的原子核具有更高的能量，所以只有当中子β衰变释放出的能量 (约0.8MeV) 足以提供这个能量差时，才能发生原子核的β衰变。否则，尽管有中子衰变的可能，原子核仍将保持稳定。

（4）强相互作用

强力是这四种力中最强的。如上所述，两个强子之间的力范围为10 -15 m。然而夸克之间的力似乎相当奇特。在短距离内，它们之间的相互作用力就像其他相互作用一样服从平方反比定律。当距离超过10 -15 m后则力就变成非常大，不再随距离而下降。这意味着，无论这两个夸克之间的距离有多远，总有一个恒定的力把它们拉回来。这也意味着将两个夸克分开所需的功和能量是与它们的距离成正比的，因此需要无限的能量来分离它们。因此，两个夸克不能彼此分离，这一性质已经被称为夸克禁闭。所以一组夸克有时是禁闭，有时不是。后面再讨论这些情况。

总之，现在人们知道，自然界存在这样几种基本粒子。费米子提供宇宙物质 (夸克和轻子) ，玻色子用来传递力(规范粒子)并提供对称性破缺。图1展示了这些粒子。物质由两种粒子组成，夸克和轻子。夸克参与强相互作用，但轻子不参与。每个夸克有3种可能的颜色，而轻子是无色的。夸克和轻子各有三代。第一代夸克为(u,  d)，第二代夸克为(c, s)，第三代夸克为(t, b)。相应的三代轻子分别是(e - , ν e )、(μ - , ν μ )和(τ, ν τ )。对于每一个夸克或轻子，都存在一个具有相同质量和电荷相反的反粒子。

自然界所有力都是四种基本相互作用的复杂表现形式，按照强度从大到小依次为强、电磁、弱和引力。引力和电磁相互作用的作用范围非常长，强相互作用和弱相互作用范围较短。从粒子物理的角度看这些基本相互作用是由基本规范粒子来传播来实现的。实际上，相互作用的的传递就是因为这些粒子可以自由地被吸收和产生。每个粒子负责传递不同类型的基本力。相应的规范粒子是传递强力的胶子(g)、传递电磁相互作用的光子(γ)、传递弱力的W ± 和Z 0 粒子以及传递引力的引力子(G)。除了引力子之外，所有其他的规范粒子现在都已经被发现了。规范粒子和希格斯粒子是玻色子。它们服从玻色-爱因斯坦的统计，并且自旋数为整数。除此之外，还有一个希格斯玻色子。

图1. 粒子物理标准模型粒子谱

至此已经讨论了粒子物理标准模型中的所有粒子：包括组成物质的费米子、传递相互作用的玻色子以及希格斯粒子。 (引力子现在还不能完全属于标准模型。) 当然这有点像是在分类列表，知其然而不知其所以然。这种组成物质、传播相互作用的基本粒子是由一个非常漂亮的理论框架来描述的，下面将详细说明标准模型。

3

量子场论与对称性

基本粒子和相互作用的理论是由量子场论来描述的。量子场论是狭义相对论与量子力学相结合而产生的理论，所研究讨论内容非常宏大，不仅在高能物理，在凝聚态、统计物理等领域场论都有广泛应用。本文主要目的是简介粒子物理标准模型，所以本节所讨论内容仅是场论的一小部分课题。

在开始正式讨论之前，必须对基本粒子的物理图像有所了解。基本粒子像是一个经典物理中类似于质点或者点电荷一样的物体。其实粒子物理中所讨论的粒子都不是经典客体，而是一个具有波粒二象性的量子客体。理解这一点是非常重要的。因为不管是经典的粒子还是经典的波，当用它们来描述微观粒子的时候，都会存在问题。比如电子本身带有电荷， 宏观上看同种电荷是相互排斥的，必须有吸引力才能让电子保持一个球或者波的形状.那么这个力是什么？难道电子和光子有更加微观的结构？而现在高能对撞机上仍然看不到电子或者光子存在什么内部结构。

因此讨论量子场论之前，我们需要理解量子力学的哲学。对量子力学的理解其实一直都是饱受争议的，20世纪上半叶玻尔和爱因斯坦之间关于量子力学理解的论战一直持续到现在 ^{[18 ]} 。当前大多数物理学家已经接受了以玻尔为首的“哥本哈根学派”提出的量子力学的解释。这个正统的量子力学解释已经基本上回答了基本粒子物理图像的理解问题。本文将不去追究这些量子力学解释的发展现状， 这里只给出哥本哈根学派的量子力学解释。

量子力学的基础是测不准原理，微观粒子具有波粒二象性。量子力学理论描述的并不是完全客观的、机械的物质世界，而是客观世界在人们不同测量的时候给出什么样结果的理论。人们对理论的表述只能应用我们可以理解的概念，而所有我们可以理解的概念都源于宏观的某个测量。根据不确定关系，这种测量越精确，人们就会丧失与之共轭的物理量的信息.所以微观粒子在实验中呈现矛盾的结果并不说明量子理论是错误的，因为理论本身就是在告诉你做怎样的测量，会有什么样的结果。量子力学并不回答在做测量之前，微观粒子到底是个什么样的存在。

如果接受了以上量子力学的解释，就可以对微观粒子的物理图像做出回答了。每种关于基本粒子如电子或者光子是什么的表述，总是对应于某种测量。所以电子和光子会给出宏观上看来完全不同的图像， 比如：(1)一个平面的电子波，电子有确定的动量，位置完全不确定，此时可以认为电子的半径是无穷大的；(2)一个确定位置的电子，半径是无穷小的，动量是完全不确定的，得到这样的电子，需要无穷大的能量；(3)金属中的自由电子气体，可以看作以金属表面为边界的驻波，满足费米狄拉克统计；(4)黑体中的光子，可以看作以黑体表面为边界的驻波，满足玻色-爱因斯坦统计。这些表述都很好地解释了观测到的实验现象，这正是量子力学几个重要验证。

这样量子力学看上去有很大的随意性，其实不是这样的。早期量子力学是以低速经典力学量子化理论为基础的，随后人们开始发展与相对论结合的量子力学，由此而建立了无穷多自由度的量子场论。量子场论中给出了物质基本相互作用的构建方法，让人们更加深刻地理解了相互作用的本质以及时空的基本属性。这些基本粒子其实就是在时空存在的一个场，场的量子化就产生了这些粒子。这些粒子就是具有波粒二象性的基本粒子。根据诺特尔定理，每个连续对称性都有相应的守恒荷与守恒流与之对应，那么时空的对称性和场所具有的所谓的内禀对称性就决定了基本粒子的属性。量子场论其实就是在这些对称性要求下存在的量子场而已，讨论基本粒子，就需要讨论对称性以及相应的守恒律。

3.1 连续对称性与规范场

时空对称性相对来说是比较简单，就是通常大学物理课堂上会讲到的内容。今天的物理和10亿年、100亿年前是一样的。地球上和宇宙的其他部分也是一样的。前者，即时间平移不变性，或时间平移对称性。根据诺特尔定理，这种对称性其实对应着能量守恒定律。后者，被称为空间平移不变性，对应的则是动量守恒定律。无论实验室是面向东方还是面向南方，我们也会得到同样的物理学。这种旋转对称性导致角动量守恒。

从时空对称性的角度看，在四维平直时空存在的场有 标量、矢量 和 旋量场 。标量场可以理解为每个时空点都有一个数值，而该数值不会因为参考系的改变而改变；矢量场就是每个时空点都有一个矢量。注意这里的矢量是四维时空矢量，不是通常电磁学教科书写的三维空间的矢量。旋量场用来描述费米子。我们知道电子有自旋。其自旋的洛伦兹变换表示出来的场就是旋量场。前两节讨论的基本粒子都是这三类场中的一个。比如费米子是旋量场，规范玻色子是矢量场。希格斯粒子是标量场。时空对称性以外这些基本粒子的场还满足内部对称性。

内部对称性，或者粒子具有的内禀属性比较复杂，所以这里还需要对对称性在量子力学及场论中的应用做一些说明。对称性在数学的分支理论群论中得到了系统的研究。对称性是由群指定的，它告诉我们量子数守恒，以及如何将它们相加。可叠加的量子数通常对应于 U (1)群。电荷就是一种 U (1)对称性，基本粒子中还有超荷也具有 U (1)对称性。 U (1)群是一个所谓的阿贝尔群，这意味着对称变换的顺序是不重要的。比如一个场 ψ 变换为

ψ → ψ ′=e iα ψ (1)

这个场仅仅乘以一个虚的相位因子，e指数上的变换参数 α 就是一个数。如果做两次变换，参数 α 1 ， α 2 可以任意交换。

向量性量子数对应于非阿贝尔群，其对称运算的顺序不能任意交换。此时变换的场有两个或者两个以上的分量组成。我们前面写的上夸克、下夸克(u，d)，电子中微子、电子 (ν e ，e)，等就是表示它们组成了一个二重态，对它们的变换的群元就是一个矩阵。比如(u，d) 变换成(u′，d′)为

(2)

这里 U 就是一个矩阵。读者应该清楚，两个矩阵相乘是不能随便交换顺序的。这就是非阿贝尔群变换。基本粒子满足的非阿贝尔群变换有：

• 弱同位旋的 SU (2)量子数 ，它在弱相互作用中起着重要作用。6个夸克形成3个弱同位旋二重态，(u，d)、(c，s)、(t，b)。6个轻子还形成了3个弱同位旋二重(e - ，ν e )、(μ - ，ν μ )和(τ，ν τ )。

• 颜色量子数 是一个与 SU (3)群 有关的向量量子数。需要说明的，虽然叫做颜色，但这与我们在日常生活中看到的颜色完全无关。6个夸克u、d、c、s、t、b中的每一个构成一个颜色三重态3，每一个反夸克构成共轭色三重态3 * 。胶子属于伴随多重态8。总之，有8个胶子，3个u夸克，3个 夸克等。

下面的问题就是，这些多重态粒子之间是怎么相互作用的。也就是构建这些场的规则是什么。这里就需要说明一下规范场论。这一理论是由杨振宁和米尔斯于1954年提出的，现在被称为 非阿贝尔规范理论 ，或杨-米尔斯理论。这是一个非常深刻也非常复杂的理论。本文做为标准模型的简单综述，就不详细说明其细节了。这里只简单说一下其理论关键点：“规范” ^{[19 ]} 的意义其实是指以上变换比如 U (1)变换的相位 α ，或者非阿贝尔变换 U 是与时空坐标( x ， y ， z ， t ) 相关的函数。这样的对称性就叫 定域规范对称性 。因为场有动能项，需要对时空坐标求导，如果要求场满足这样的对称性，那对场时空求导的规范变换就存在问题。比如对 ψ

(3)

由于群参数 α 是空间坐标的函数，对其求导也会多出一个项来。规范场论就是通过引入一个伴随表示矢量场变换来吸收掉这个多出来的因子。杨-米尔斯理论描述的就是定域非阿贝尔规范场理论。这样自然就可以得到矢量场与费米场的耦合。也就得到了由内部对称性决定的相互作用的理论了。所以所谓的粒子物理标准模型其实就是将实验测定的各种对称性按照非阿贝尔规范理论的形式写下来而已。组成物质的费米子是变换群的自身表示，传递相互作用玻色子是伴随表示。但是事情并不是那么简单。这是因为除了定域非阿贝尔对称性这种连续的对称性之外，基本粒子还具有分立对称性，而且这些对称性并不一定严格守恒。

3.2 分立对称性

分立对称性是场做分立变换的对称性，比如空间翻转

x → x ′=- x (4)

这样的变换不能由一个连续的参数来表达，因此是分立的。这种对称性产生一个守恒的量子数，称为 宇称 。1957年，李政道和杨振宁发现，强相互作用和电磁相互作用中宇称守恒，弱相互作用中宇称破坏。这是什么意思？其实后来的实验发现参与弱相互作用的粒子其实都是左手粒子。理解这个物理现象需要深入理解空间翻转变换的对称性。

图2展示空间翻转变换的示意图。左图 xyz 轴满足右手螺旋准则，右图 xyz 轴满足的则是左手螺旋准则。不能通过连续变换，把左图变为右图，只有做镜像变换才可以做到。类似于此，我们可以把各种基本粒子的量子场定义左手粒子和右手粒子。实验发现，弱相互作用中左右手粒子相互作用是不一样的。换句话说， 在弱相互作用下，宇称不是守恒量子数 。当然这里面的情况会非常复杂，因为左右手还可以有一个连续变换来定义。比如粒子自旋方向由粒子运动方向之间的关系也可以定义左旋粒子和右旋粒子。这种定义被称为螺旋度。对于无质量粒子，螺旋度是确定的。而有质量粒子，只能存在近似的螺旋度。因为如果存在质量的话，总是可以存在洛伦兹变换改变动量的方向。

图2. 宇称变换对应的手征对称性

还有其他的一些分立对称性，比如 电荷共轭变换 ，即把粒子变为它们的反粒子的变换。这种变换对应的量子数也被称为C宇称。把电子变换为正电子，就是一个电荷共轭变换。注意γ，Z 0 ，H 0 是自己的反粒子，W + 和W - 互为反粒子。 弱相互作用也违背电荷共轭不变性 ，因为相互作用发生在左手夸克和轻子上，而左手反夸克和反轻子不发生相互作用。参与相互作用的是右旋反夸克和反轻子。所以C宇称也破坏了。

另外还有一类通常并没有明确说明，但是也严格守恒的分立对称性。实验中发现有3个夸克组成的强子具有重子数，通常取为1。也就是说，夸克的重子数是1/3。 相关粒子物理过程中， 重子数不会发生改变 。如果产生更多的重子，则必定是正反重子数相互抵消，以保持反应前后重子数不变。介子都是由正反夸克组成的，不具有重子数，则在各种物理过程中，产生的介子数目不受重子数目的影响。类似地，轻子具有轻子数。比如定义电子轻子数是1，电子中微子轻子数是-1。注意每一代的轻子数是不同的。 轻子物理过程中，每代的轻子数守恒 。所以β衰变中，中子 (重子数1) 衰变成了质子 (重子数1) 、电子 (轻子数1) 和反电子中微子 (轻子数-1) 。而不是电子中微子。

这些分立对称性对应的量子数也是构建粒子物理标准模型需要遵循的原则。既然弱相互作用下粒子宇称不守恒，那相互作用的模型就是一个手征理论。所谓手征理论说的就是模型中左手和右手粒子的相互作用是不一样的。换一种说法，在上面讲的杨-米尔斯理论中，如果左右手粒子相互作用不一样，那模型就没有质量项。而通常的基本粒子很多都是有静止质量的。不仅如此，还存在另外一个问题。为什么强相互作用和弱相互作用力程很短？现在我们知道弱相互作用力程很短是因为传播弱相互作用的规范玻色子质量很大，而杨-米尔斯理论中规范粒子也不能写下质量项，那怎么才能构建一个合理的模型呢？这时候就轮到希格斯机制出场了。

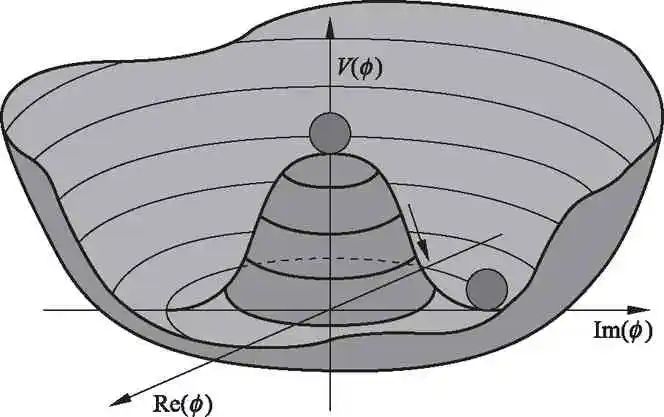
撇开复杂的数学运算，通常的物理教材都用图3来讲解 希格斯机制 。这里要引进一个标量场 (自旋0) 粒子，它的势就如图3中所示的啤酒瓶底形状。这样的势使得粒子场值等于零(中心点)处不稳定，而真空会跑到边上势值最低点位置。这样真空对称性就自发破缺了，规范粒子吃掉歌德斯通粒子 ^{[20 ]} (无质量的玻色子) 获得了质量。费米子也可以由其与标量粒子的耦合产生质量。该标量场在真空点处激发会产生一个自旋为零的粒子，就是所谓的希格斯粒子。这是标准模型理论重要的理论基础。这种获得质量的方式有时也被称为真空凝聚。

图3. 真空对称性自发破缺

可能有读者对以上的简单说明有所困惑：那此时模型中的规范对称性还有没有？杨-米尔斯理论还能不能用？其实还有另外一个比较通俗的方式来理解希格斯机制，即真空与介质中的光速。我们知道，真空中光速是不变的，恒定为 c

请到「今天看啥」查看全文