正文
坚持。
于是,同样是学习中遇到难题,前者可能畏难而放弃,认为没必要研究那么难的问题;而后者则会仔细钻研,然后干掉大BOSS,暴涨一波经验值,在滚雪球的挑战与成就感中达到越来越高的等级。
事后,很多人就会觉得这是天赋,是智商。
学习,本身就是一种积累的过程。很多人误以为学习这个动作只是在积累路程,大错特错。
学习也能积累学习的速度
——换言之,
学习本身是自带微小的加速度的
。
越学习,就越适
应学习,越在“放纵/学习”的艰难抉择中选择后者,你对后者的突触建立就更强一分,下次
选择坚持学习也就不那么痛苦一些。
所
以,我一向认为,那些说什么“能够努力也是一种天赋”的,不是思维过于简单,就是在为自己的懒惰找借口。
当然,更不用说学习本身还能让你积累试错经验,改进学习方式了。
————
以上的论证,仅能证明“
后天养成的学习习惯能为学习效率产生巨大贡献
”,并不意味着“
学习效率高的人一定拥有好的学习习惯
”。
我知道很多人会举XXX天天上课吊儿郎当回宿舍就打游戏照样年级前十……等等的例子。所以,接下来就要说到另一种因素——
思维习惯
。
这种因素更重要,也同时更隐蔽。
思维习惯有多重要?
我们在接受一个新的经验或新的理论时,对其的认知往往是依靠其与已知的经验或理论进行的比较与联系。
许多关于学习原理的书都会讲到这一点,并由此强调体系,比喻等等的重要性,但很多人并未真正理解这是怎么回事。
而对于这种思维习惯的获取,后天教育中一个作用相当大的途径就是
阅读习惯的养成
。
按照《如何阅读一本书》中的分法,书籍的作用有两种,一是提供经验、二是教授理论。
比如一部小说,就是一系列经过高度整理,高度有序化的经验;一本科普杂志,除了经验之外还有一系列浅显通俗的理论。
一个热爱阅读小说新闻的孩子,在早期可能就通过阅读这种可以最快提升自己经验丰富度的途径,拥有了远超其他同龄人的
早期经验积累
,而人总有从已有经验归纳理论的倾向。
这个过程好比核裂变里中子的释放一样——物质体积越大,发生中子撞击的可能性也就越大。人的经验越丰富,平时突发灵感从经验归纳出理论/联系的可能性也就越大。面对新知识时也就更容易触类旁通,举一反三。
一个热爱阅读科普杂志或者浅显理论的孩子,则更容易养成锻炼出自己
接受外来理论与整理既有经验的习惯
。
同时一个个由以往经验整理出理论的成功案例很可能会在价值观上激励他们思考,并养成强烈的思考倾向。
你仔细观察那些学习效率高的人,很可能也会发现其小时候或多或少都有爱阅读的习惯。无论是何种阅读,都有产生精神愉悦的可能。
而这种愉悦将成为宝贵的早期正向激励,使其爱上吸收外界经验/接受外界理论,或者开始看到一道难题就忍不住思考,忍不住推敲。
细分起来,
他们可能也因此爱上数学/物理/天文/历史等等具体的领域。所谓兴趣,很大程度上也是后天的。而兴趣对一个人学习的作用,不言而喻。
然后,你可能会说,许多天才长于逻辑推理或数学计算这些比较先验的东西,这又如何解释?
这里引用@张英锋的答案
智商高低是因为思维习惯不同造成的吗?
- 张英锋的回答:
成年后的高斯说,在他学会说话之前就会计算了。这说明在高斯的幼年经常接触到各种数字,无意间让他很小的年龄就掌握了初等算术。有这样一个有数学应用背景的父亲就是拼爹,但高斯的父亲有个缺点就是目光短浅。
通过长期高强度的数学计算,高斯不仅计算能力极强,而且非常善于发明数学工具,来简化自己的计算过程。刚才说到高斯9岁时就掌握了等差数列的速算方法,他 在18岁时又发明了最小二乘法,极大简化了计算过程。后来,勒让德在54岁时也发明了最小二乘法,并早于高斯发表,获得了优先权,但这个工具高斯已经用了 十几年。 但是没有公开!
有人曾估算,如果高斯当时能及时发表他的研究成果,整个高等数学可以向前推进50年!但高斯是个完美主义者,他拒绝发布不完整和有瑕疵的作品。他的很多成果都来自内在视觉洞察力,是直觉形式的结论,虽然他自己长期使用,已被验证没有问题,但并没有经过逻辑严密的证明。而高斯跑的太快,完全不想停下来,把宝贵的时间消耗到琐碎无比的严密证明上。如果高等数学真的因此被推迟了50年,这可真是整个科学界不可估量的巨大损失!
我前面说道,数学家可以不借助纸笔来思考数学问题,这其实来源于他们高强度的数学计算,高斯是这方面的佼佼者。可能很多人会好奇,高斯的计算强度究竟有多大?我们以1818年高斯担任丹麦的测地工作为例,整个工作持续了8年,高斯白天测绘,晚上计算,他曾估计测绘所画的图就有100多万张。野外实测数据汇总后,全部计算工作由高斯负责,随便两个点都是用最小二乘法通过冗长的计算获得,一般需要一个计算能力中等的人计算2~3天才能算完,共有3000多个坐标点,总计算量需要这个人一天不休的计算10年!
也就是说,即使是逻辑推理与数学直觉这种东西,也是可以通过
后天的思维训练
锻炼的。
比如说,同样解决一道难题/理解一个难的概念,需要经过至少七层嵌套的逻辑。
于是一个经过高度逻辑训练的人,
可能前三层逻辑早已烂熟于心,第四五层逻辑又在他以前做过的题目/看过的书中熟悉过,
剩下的工作只不过是推出剩下的两层逻辑而已;
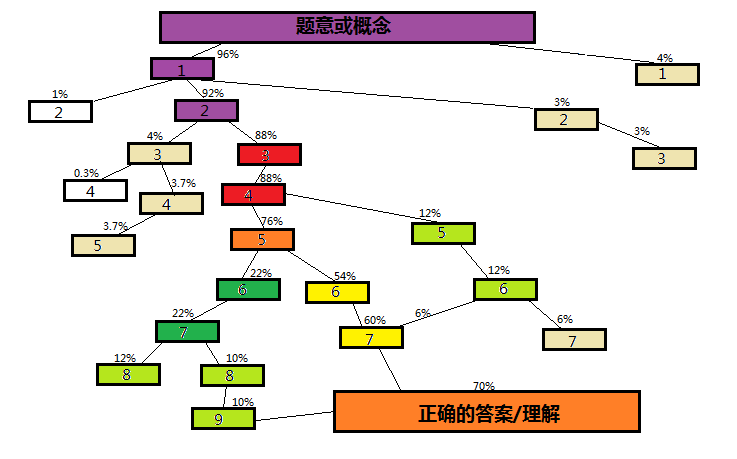
而一个没经过高度逻辑训练的人,可能只能熟悉前两层的逻辑,于是要解决这个问题,
他可能就要占用极大的工作记忆空间,经历无数次试错,承受大量不熟悉逻辑的痛苦,才能HOLD住那高达五层的逻辑树。
于是解不出来就是很正常的事了。





