正文
在证明GAN能够做得拟合真实分布时,Goodfellow做了一个很大胆的假设:用来评估样本真实度的Discriminator网络(下文称D-网络)
具有无限的建模能力,
也就是说不管真实样本和生成的样本有多复杂,D-网络都能把他们区分开。这个假设呢,也叫做
非参数假设
。
当然,对于深度网络来说,咱只要不断的加高加深,这还不是小菜一碟吗?深度网络擅长的就是干这个的么。
但是,正如WGAN的作者所指出的,一旦真实样本和生成样本之间重叠可以忽略不计(这非常可能发生,特别当这两个分布是低维流型的时候),而又由于D-网络具有非常强大的无限区分能力,可以完美地分割这两个无重叠的分布,这时候,经典GAN用来优化其生成网络(下文称G-网络)的目标函数--JS散度-- 就会变成一个常数!
我们知道,深度学习算法,基本都是用梯度下降法来优化网络的。一旦优化目标为常数,其梯度就会消失,也就会使得无法对G-网络进行持续的更新,从而这个训练过程就停止了。这个难题一直一来都困扰这GAN的训练,称为
梯度消失
问题。
WGAN来袭
为解决这个问题,WGAN提出了取代JS散度的Earth-Mover(EM)来度量真实和生成样本密度之间的距离。该距离的特点就是,即便用具有无限能力的D-网络完美分割真实样本和生成样本,这个距离也不会退化成常数,仍然可以提供梯度来优化G-网络。不过WGAN的作者给出的是定性的解释,缺少定量分析,这个我们在后面解释LS-GAN时会有更多的分析。
现在,我们把这个WGAN的优化目标记下来,下文我们会把它跟本文的主角LS-GAN 做一番比较。
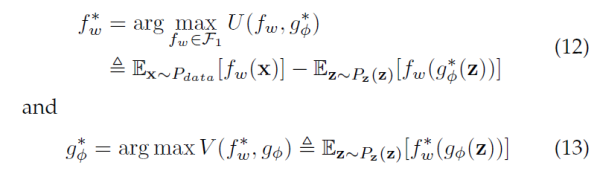
这里 f-函数和 g-函数 分别是WGAN的批评函数(critics)和对应的G-网络。批评函数是WGAN里的一个概念,对应GAN里的Discriminator。该数值越高,代表对应的样本真实度越大。
好了,对WGAN就暂时说到这里。总结下,由于假设中的
无限建模能力,
使得D-网络可以完美分开真实样本和生成样本,进而JS散度为常数;而WGAN换JS散度为EM距离,解决了优化目标的梯度为零的问题。
不过细心的读者注意到了,WGAN在上面的优化目标(12)里,有个对f-函数的限定:它被限定到所谓的Lipschitz连续的函数上的。那这个会不会影响到上面对模型
无限建模能力的
假设呢?
其实,这个对f-函数的Lipschitz连续假设,就是沟通LS-GAN和WGAN的关键,因为LS-GAN就是为了限制GAN的
无限建模能力
而提出的。
熟悉机器学习原理的朋友会知道,一提到
无限建模能力,
第一反应就应该是条件反应式的反感。为什么呢?无限建模能力往往是和过拟合,无泛化性联系在一起的。
仔细研究Goodfellow对经典GAN的证明后,大家就会发现,之所以有这种无限建模能力假设,一个根本原因就是GAN没有对其建模的对象--真实样本的分布--做任何限定。
换言之,GAN设定了一个及其有野心的目标:就是希望能够对各种可能的真实分布都适用。结果呢,就是它的优化目标JS散度,在真实和生成样本可分时,变得不连续,才使得WGAN有了上场的机会,用EM距离取而代之。
所以,某种意义上,
无限建模能力正是一切麻烦的来源。
LS-GAN就是希望去掉这个麻烦,取而代之以“按需分配”建模能力。
LS-GAN和“按需分配”的建模能力
好,让我们换个思路,直接通过限定的GAN的建模能力,得到一种新的GAN模型。这个就是LS-GAN了。我们先看看LS-GAN的真容: