正文
这类数据库会使用哈希表,哈希表中有一个特定的键指向一个特定的值,KeyValue的特点是去中心化,不涉及业务关系。代表Redis。
这类数据库用于分布式海量存储,和KeyValue的区别在于这里的Key指向的是列。横向拓展性好,适合大数据量高IO。代表HBase,Cassandra
属于KeyValue数据库的升级版,允许嵌套键值。文档是处理信息的基本单位,一个文档等于一个关系数据库的一条记录。
因为文档的自由性,文档型数据库适合复杂、松散、无结构或半结构化的数据模型,和JSON类似,叫做BSON(MongoDB的存储格式)。代表MongoDB
基于图论算法的数据库,将数据集以图形元素(点、线、面)建立起来。这种数据库常应用在社交网络关系链,N度关系等。代表Neo4j
正则表达式(Regular Expression)
正则表通常被用来检索、替换那些符合某个模式(规则)的字符串。通过特定字符的组合,对字符串进行逻辑过滤。例如注册账号时检查对方邮件格式对不对啊,手机号格式对不对啊。
学起来靠记,记了也会忘,每次用得查,查了还得检验。网上记忆口诀一堆图表,相关网站也不少,仁者见仁了。

Vendor Landscape
不懂,供应商风景?
Env Setup
环境安装
想了半天,Env应该是环境安装的意思,IDE啊,GUI啊等等全部安装上去,再调各种路径啥的。针对数据科学家,Anaconda +Rstudio用的比较多。
——————
Statistics 统计
统计是数据科学家的核心能力之一,机器学习就是基于统计学原理的,我不算精通这一块,许多内容都是网络教科书式的语言。都掌握后再重写一遍。
Pick a Dataset(UCI Repo)
找数据(UCI数据集)
UCI数据库是加州大学欧文分校(Universityof CaliforniaIrvine)提出的用于机器学习的数据库,这个数据库目前共有335个数据集,其数目还在不断增加,可以拿来玩机器学习。网上搜的到。另外的数据来源是Kaggle竞赛等。
最经典的数据莫过于Iris了。
Descriptive Statistics(mean, median, range, SD, Var)
描述性统计(均值,中位数,极差,标准差,方差)
均值也叫平均数,是统计学中的概念。小学学习的算数平均数是其中的一种均值,除此以外还有众数和中位数。
中位数可以避免极端值,在数据呈现偏态的情况下会使用。
极差就是最大值减最小值。
标准差,也叫做均方差。现实意义是表述各数据偏离真实值的情况,反映的是一组数据的离散程度。平均数相同的两组数据,如[1,9]和[4,6],平均数相同,标准差不一样,前者的离散程度更大。
方差,是标准差的平方。方差和标准差的量纲是一致的。在实际使用过程中,标准差需要比方差多一步开平方的运算,但它在描述现实意义上更贴切,各有优劣。
Exploratory Data Analysis
探索性数据分析
获得一组数据集时,通常分析师需要掌握数据的大体情况,此时就要用到探索性数据分析。
主要是两类:
探索性数据分析不会涉及到复杂运算,而是通过简单的方式对数据有一个大概的了解,然后才去深入挖掘数据价值,在Python和R中,都有相关的summary函数。
Histograms
直方图
它又称质量分布图,是一种表示数据分布的统计报告图。
近似图表中的条形图,不过直方图的条形是连续排列,没有间隔、因为分组数据具有连续性,不能放开。
正常的直方图是中间高、两边低、左右近似对称。而异常型的直方图种类过多,不同的异常代表不同的可能情况。
Percentiles & Outliers
百分位数和极值
它们是描述性统计的元素。
百分位数指将一组数据从小到大排序,并计算相遇的累积百分值,某一百分位所对应数据的值就称为这一百分位的百分位数。比如1~100的数组中,25代表25分位,60代表60分位。
我们常将百分位数均匀四等分:第25百分位数,叫做第一四分位数;第50百分位数,称第二四分位数,也叫中位数;第75百分位数,叫做第三四分位数。通过四分位数能够简单快速的衡量一组数据的分布。它们构成了箱线图的指标。
极值是最大值和最小值,也是第一百分位数和第一百百分位数。
百分位数和极值可以用来描绘箱线图。
Probability Theory
概率论,统计学的核心之一,主要研究随机现象发生的可能性。
Bayes Theorem
贝叶斯定理
它关于随机事件A和B的条件概率的定理。
现实世界有很多通过某些信息推断出其他信息的推理和决策,比如看到天暗了、蜻蜓低飞了,那么就表示有可能下雨。这组关系被称为条件概率:用P(A|B)表示在B发生的情况下A发生的可能性。
贝叶斯公式:P(B|A) = P(A|B)*P(B) / P(A)
现实生活中最经典的例子就是疾病检测,如果某种疾病的发病率为千分之一。现在有一种试纸,它在患者得病的情况下,有99%的准确判断患者得病,在患者没有得病的情况下,有5%的可能误判患者得病。现在试纸说一个患者得了病,那么患者真的得病的概率是多少?
从我们的直觉看,是不是患者得病的概率很大,有80%?90%?实际上,患者得病的概率只有1.9%。关键在哪里?一个是疾病的发病率过低,一个是5%的误判率太高,导致大多数没有得病的人被误判。这就是贝叶斯定理的作用,用数学,而不是直觉做判断。
最经典的应用莫过于垃圾邮件的过滤。
Random Variables
随机变量
表示随机试验各种结果的实际值。比如天气下雨的降水量,比如某一时间段商城的客流量。
随机变量是规律的反应,扔一枚硬币,既有可能正面、也有可能反面,两者的概率都是50%。扔骰子,结果是1~6之间的任何一个,概率也是六分之一。虽然做一次试验,结果肯定是不确定性的,但是概率是一定的。随机变量是概率的基石。
Cumul Dist Fn(CDF)
累计分布函数(Cumulative Distribution Function)
它是概率密度函数的积分,能够完整描述一个实数随机变量X的概率分布。直观看,累积分布函数是概率密度函数曲线下的面积。
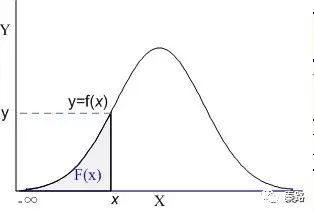
上图阴影部分就是一个标准的累积分布函数F(x),给定任意值x,计算小于x的概率为多大。实际工作中不会涉及CDF的计算,都是计算机负责的。记得在我大学考试,也是专门查表的。
现实生活中,我们描述的很多概率都是累积分布函数,我们说考试90分以上的概率有95%,实际是90分~100分所有的概率求和为95%。
Continuos Distributions(Normal, Poisson, Gaussian)
连续分布(正态、泊松、高斯)
分布有两种,离散分布和连续分布。连续分布是随机变量在区间内能够取任意数值。
正态分布是统计学中最重要的分布之一,它的形状呈钟型,两头低,中间高,左右对称。
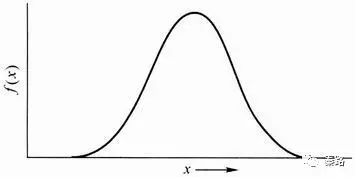
正态分布有两个参数,期望μ和标准差σ:μ反应了正态分布的集中趋势位置,σ反应了离散程度,σ越大,曲线越扁平,σ越小,曲线越窄高。
自然届中大量的现象都按正态形式分布,标准正态分布则是正态分布的一种,平均数为0,标准差为1。应用中,都会将正态分布先转换成标准正态分布进行计算。很多统计学方法,都会要求数据符合正态分布才能计算。
泊松分布是离散概率分布。适合描述某个随机事件在单位时间/距离/面积等出现的次数。当n出现的次数足够多时,泊松分布可以看作正态分布。

高斯分布就是正态分布。
Skewness
偏度
它是数据分布倾斜方向和程度的度量,当数据非对称时,需要用到偏度。
正态分布的偏度为0,当偏度为负时,数据分布往左偏离,叫做负偏离,也称左偏态。反之叫右偏态。

ANOVA
方差分析
用于多个变量的显著性检验。基本思想是:通过分析研究不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小。
方差分析属于回归分析的特例。方差分析用于检验所有变量的显著性,而回归分析通常针对单个变量的。
Prob Den Fn(PDF)
概率密度函数
PDF是用来描述连续型随机变量的输出值。概率密度函数应该和分布函数一起看:

蓝色曲线是概率密度函数,阴影部分是累积分布函数。我们用概率密度函数在某一区间上的积分来刻画随机变量落在这个区间中的概率。概率等于区间乘概率密度,累积分布等于所有概率的累加。
概率密度函数:f(x) = P(X=x)
累积分布函数:F(x) = P(X
概率密度函数是累积分布函数的导数,现有分布函数,才有密度函数。累积分布函数即可以离散也可以连续,而密度函数是用在连续分布中的。
Central Limit THeorem
中心极限定理
它是概率论中最重要的一类定理。
自然届中很多随机变量都服从正态分布,中心极限定理就是理解和解释这些随机变量的。我们有一个总体样本,从中取样本量为n的样本,这个样本有一个均值,当我们重复取了m次时,对应有m个均值,如果我们把数据分布画出来,得到的结果近似正态分布。





