正文
好多了!虽然仍然随机放置,但单元的大小更一致。尽管样品的数量(6667)保持不变,但由于它们均匀分布,保留了更多的细节和引入了更少的噪声。如果你眯着眼睛,几乎可以弄清楚原来的笔触。
我们可以使用Voronoi图来更直观地研究样本分布,通过根据其面积给每个单元上色。较暗的单元较大,表示稀疏采样; 较浅的单元较小,表明密集采样。最佳图案具有几乎均匀的颜色,同时保持不规则的采样位置。(显示单元面积分布的直方图也是很好的,但是Voronoi具有同时显示采样位置的优点)。
这是同样的6667个采样点的不均匀随机采样:

黑点是采样点之间的大空隙,可能是由于欠采样导致的视觉局部缺陷。相同数量的最佳候选样品在单元面积中表现出小得多的变化,并且因此着色更一致:

我们能做得比最佳候选算法更好吗?是的! 我们不仅可以用不同的算法产生更好的样本分布,而且这种算法更快(线性时间)。它至少像最佳候选算法一样容易实现。这种算法甚至可以扩展到任意维度。
这个奇迹叫做Bridson的泊松盘采样算法,它看起来像这样:

该算法的功能明显不同于其他两个——它充分利用现有采样点逐步生成新的采样点,而不是在整个采样区域随机生成新的采样点。这使其进展具有准生物学外观,如在培养皿中分裂的细胞。注意,也没有采样点彼此太接近;这是定义由算法实施的泊松盘分布的最小距离约束。
这就是它的工作原理:
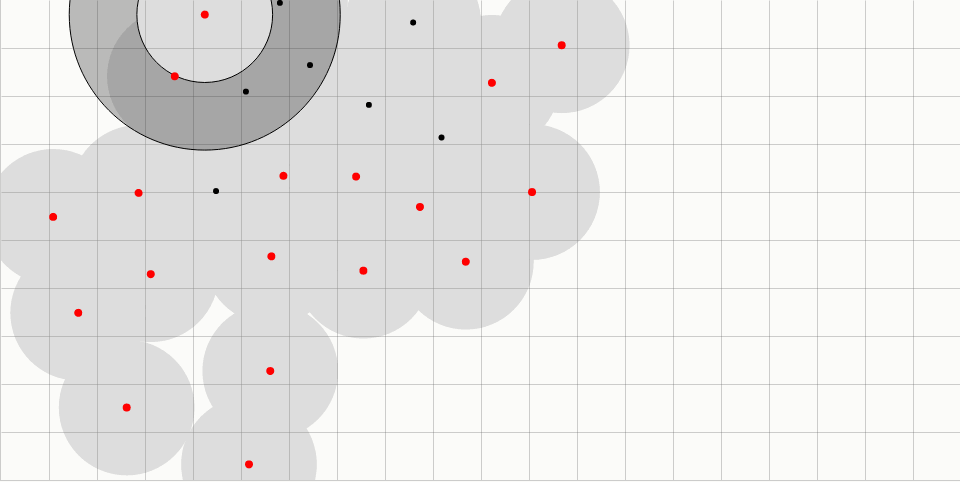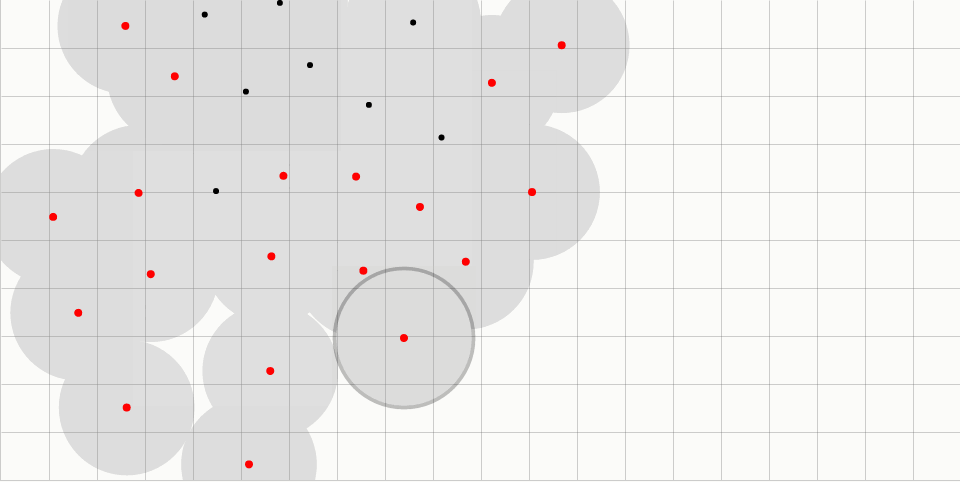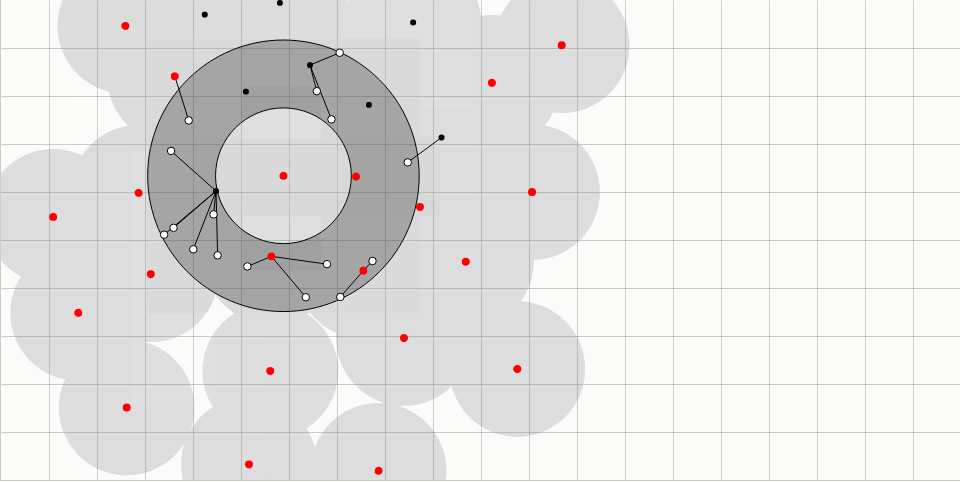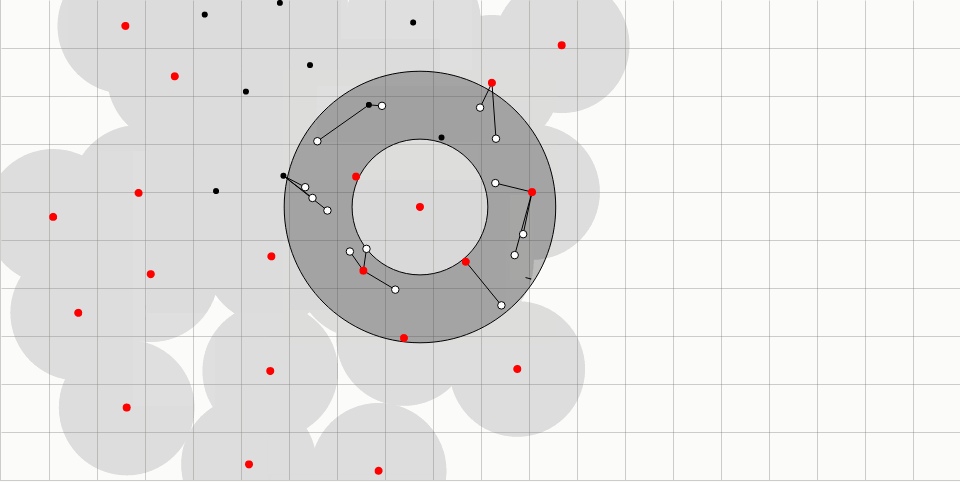
红点表示“活跃”采样点。在每次迭代中,从所有活跃采样点的集合中随机选择一个。然后,在围绕所选采样点的环内随机生成一些数量的候选采样点(用空心黑点表示)。环从半径r延伸到2r,其中r是样本之间的最小允许距离。
来自现有采样点的距离r内的候选采样点被拒绝;这个“禁止区”以灰色显示,用黑线连接将被拒绝的候选采样点和附近的现有采样点。网格加速每个候选采样点的距离检查。网格尺寸r /√2确保每个单元可以包含至多一个采样点,并且仅需要检查固定数量的相邻单元。
如果候选采样点是可以接受的,它被添加作为一个新的采样点,然后随机选择一个新的活跃采样点。如果没有一个候选采样点是可以接受的,所选择的活跃采样点被标记为无效(颜色从红色变为黑色)。当没有采样点保持活跃时,该算法终止。
面积用着色表示的Voronoi图显示了泊松盘采样算法相对于最佳候选算法的改进,没有深蓝色或浅黄色细胞:

泊松盘采样下的《星夜》最大地保留了细节和引入了最少的噪音。它让人想起美丽的罗马马赛克:

现在,你已经看到了一些例子,
让我们简要地思考一下为什么要把算法可视化。
▼
娱乐
我发现可视化的算法有无穷的魅力,甚至令人着迷。特别是在涉及随机性时。虽然这看似是一个牵强的理由,但不要低估了快乐的价值!此外,尽管这些可视化甚至在不理解基础算法的情况下也可以参与,但是掌握算法的重要性可以给出更深的理解。
▼
教学
你发现代码或动画更有帮助吗?伪代码( 不能编译的代码的委婉语)怎么样? 虽然形式描述在明确的文档中有它的位置,可视化可以使直观的理解更容易。
▼
调试
你有没有实现基于形式描述的算法? 可能很难! 能够看到你的代码在做什么可以提高生产力。 可视化不能取代测试需求,但测试主要用于检测故障而不是解释它。即使输出看起来正确,可视化还可以在实现过程中发现意外的表现(参看Bret Victor的《可学习的编程》和为了优秀的相关工作的《发明原理》)。
▼
学习
即使你只是想为自己学习,可视化会是一个很好的方式来得到深刻的理解。教学是最有效的学习方法之一,实现可视化就像教自己。我发现看到它,而不是熟记小而容易忘记细节的代码,更容易直观地记住一个算法。
洗牌是随机重新排列一组元素的过程。例如,你可以在打牌之前洗牌。一个好的洗牌算法是无偏的,其中每个排序都有相同的可能性。
Fisher-Yates shuffle是一个最佳的洗牌算法。 它不仅是无偏的,而且在线性时间内运行,使用恒定的空间,并且易于实现。
▼代码如下——
function shuffle(array) {
varn = array.length, t, i;
while (n) {
i= Math.random() * n-- | 0; // 0
≤
i
t= array[n];
array[n] = array[i];
array[i] = t;
}
return array;
}
以上是代码,下面是一个可视化的解释:

每一条线代表一个数字,数字小向左倾斜,数字大就向右倾斜。(请注意,你可以对一组任何东西进行洗牌,不只是数字,但这种可视化编码对于显示元素的顺序很管用。它的灵感来自于Robert Sedgwick的《用C语言实现的算法》中的排序可视化。
该算法把数组划分为两个部分,右半边是已洗牌区域(用黑色表示),左半边是待洗牌区域(用灰色表示)。每一步从左边的待洗牌区域随机选择一个元素并将其移动到右侧,已洗牌区域元素数量扩大了1个。左半边的初始顺序不必保留,这样给已洗牌区域的新元素提供了空间,该算法可以简单地讲元素交换到位。最终所有的元素都被洗牌,算法终止。
如果Fisher–Yates是一个很好的算法,那么一个不好的算法是什么样的?
▼
这是一个——
//
不要这么做!
function shuffle(array) {
return array.sort(function(a, b) {
return Math.random() - .5; // ಠ_ಠ
});
}
这种方法利用排序通过指定随机比较器函数来洗牌。比较器定义元素的顺序。它使用参数a和b (要比较的数组中的两个元素),如果a小于b,则返回小于零的值,如果a大于b,则返回大于零的值,如果a和b相等,则返回0。比较器在排序期间重复调用。
如果不给array.sort指定一个比较器,元素按照字典序列排序。
在这里,比较器返回一个在-0.5和+0.5之间的随机数。假设这定义了一个随机顺序,那么排序会随机地混杂元素并实施好的洗牌。
不幸的是,这个假设是有缺陷的。随机成对顺序(对于任何两个元素)不会为一组元素建立随机顺序。比较器必须遵守传递性:如果a> b和b> c,则a> c。但随机比较器返回一个随机值,违反了传递性,并导致array.sort的行为是未定义的!可能你会有运气,也可能没有。
它怎么不好呢?我们可以通过可视化输出来试着回答这个问题:
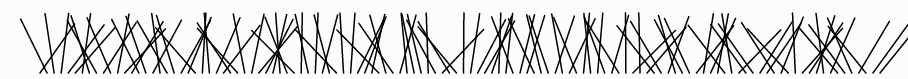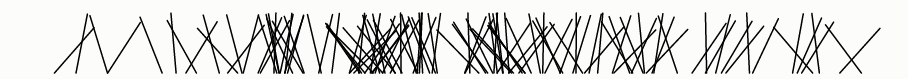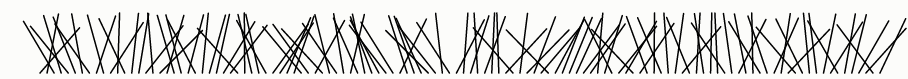
该算法不好的另一个原因是排序需要O(n lg n)时间,使得它显著地慢于只需要O(n)时间的Fisher-Yates算法。但是速度缺陷比偏差缺陷小。
这可能看起来是随机的,因此你可能会得出结论,随机比较器洗牌足够好了,并不再关注偏差,看作是迂腐的。但看起来可能会误导!有许多对人眼来说看起来是随机的,但实际上是非随机的。















