正文
i² = -1
。
因此, i 就是意味着逆时针旋转90°,-i 就是顺时针旋转90°。
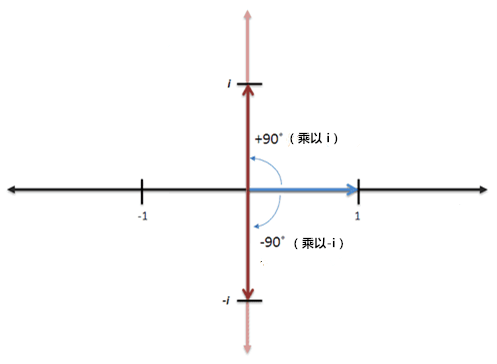
下面这个图就很直观的表达了关于
i 的运算
。
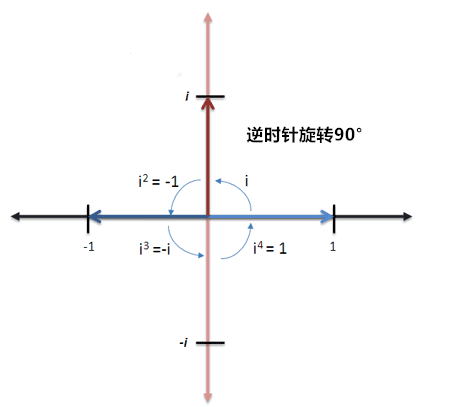
也许会有人觉得困惑:为什么要给-1开平方?这样转换来转换去的到底有什么用?
别急,我们先讲讲
复数
的定义。
现在,我们将纵轴作为虚数轴,横轴作为实数轴。
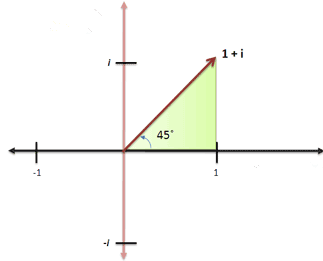
如果我们不是旋转90°,而是旋转45°的话,就得到了
1+i
。
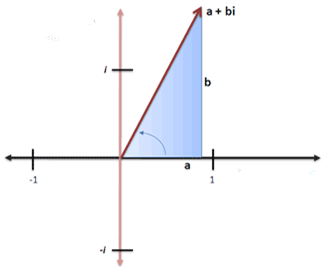
任意实数旋转某一个角度所得到的点就用
a+bi
来表示,这就是复数的定义式
。
虚数的引入,大大方便了
涉及到旋转的计算
。
比如,物理学需要计算"力的合成"。假定一个力是 3 + i ,另一个力是 1 + 3i ,请问它们的合成力是多少?
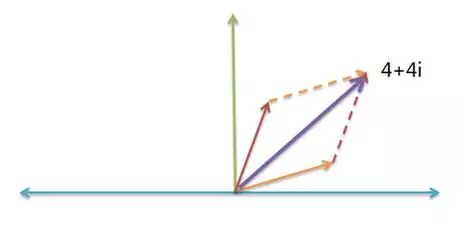
根据"平行四边形法则",你马上得到,合成力就是 ( 3 + i ) + ( 1 + 3i ) = ( 4 + 4i )。
这就是
虚数加法的物理意义
。
如果涉及到旋转角度的改变,处理起来更方便。
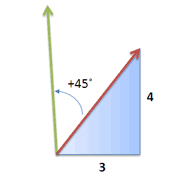
假设我们现在一艘船上,船的航向是 3 + 4i ,我们现在将船的航向逆时针旋转45°,那么,我们最新的航向应该如何表示?
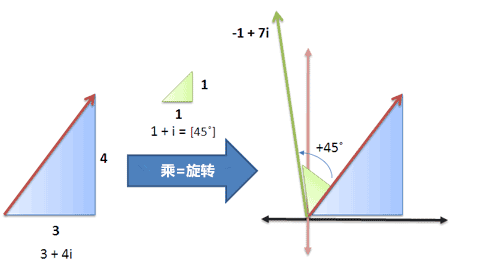
45°的航向就是 1 + i 。计算新航向,只要把这两个航向 3 + 4i 与 1 + i 相乘就可以了。
(为什么要相乘呢?)
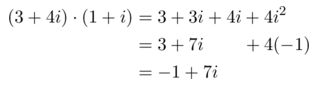
所以,新的航向就是
-1 + 7i 。
这就是
虚数乘法的物理意义:
改变旋转角度
。





