【高中物理】考点大放送~带电粒子在复合场中的运动

正文

请到「今天看啥」查看全文

解①②③式得： h ＝ B ² qL ² ／ 8n ² mE （ n ＝ l 、 2 、 3 ……）

【例 2 】如图所示，在宽 l 的范围内有方向如图的匀强电场，场强为 E ，一带电粒子以速度 v 垂直于电场方向、也垂直于场区边界射入电场，不计重力，射出场区时，粒子速度方向偏转了θ角，去掉电场，改换成方向垂直纸面向外的匀强磁场，此粒子若原样射入磁场，它从场区的另一侧射出时，也偏转了θ角，求此磁场的磁感强度 B ．

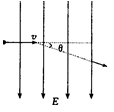
解析：粒子在电场中运行的时间 t ＝ l ／ v ；加速度 a ＝ qE ／ m ；它作类平抛的运动．有 tg θ =at/v=qEl/mv ² ………①

粒子在磁场中作匀速圆周运动由牛顿第二定律得： qvB=mv ² /r ，所以 r=mv/qB

又 ： sin θ =l/r=lqB/mv ………②

由①②两式得： B=Ecos θ /v

【例 3 】初速为零的离子经过电势差为 U 的电场加速后，从离子枪 T 中水平射出，经过一段路程后进入水平放置的两平行金属板 MN 和 PQ 之间．离子所经空间存在一磁感强度为 B 的匀强磁场，如图所示．（不考虑重力作用），离子荷质比 q/m （ q 、 m 分别是离子的电量与质量）在什么范围内，离子才能打在金属板上？

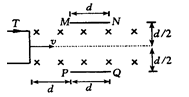
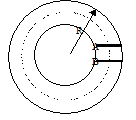
解析 ：离子在磁场中做匀速圆周运动，作出两条边界轨迹 和 TQ ，分别作出离子在 T 、 P 、 Q 三点所受的洛伦兹力，分别延长之后相交于 O ₁ 、 O ₂ 点，如图所示， O ₁ 和 O ₂ 分别是 TP 和 TQ 的圆心，设 R ₁ 和 R ₂ 分别为相应的半径．

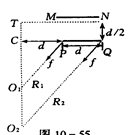
离子经电压 U 加速，由动能定理得． qU ＝ ½mv ² ………①

由洛伦兹力充当向心力得 qvB=mv ² /R ………② 由①②式得 q/m=2U/B ² R ²

由图直角三角形 O ₁ CP 和 O ₂ CQ 可得

R ₁ ² ＝ d ² ＋（ R ₁ 一 d/2 ） ² ， R ₁ ＝ 5d/4 ……④

R ₂ ² ＝（ 2d ） ² ＋（ R ₂ 一 d/2 ） ² ， R ₂ ＝ 17d/4 ……⑤

依题意 R ₁ ≤ R ≤ R ₂ ……⑥ 由③④⑤⑥可解得

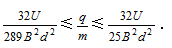
【例 4 】如图，两个共轴的圆筒形金属电极，外电极接地，其上均匀分布着平行于轴线的四条狭缝 a 、 b 、 c 和 d ，外筒的半径为 r ₀ 。在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场，磁感强度的大小为 B 。在两极间加上电压，使两圆筒之间的区域内有沿半径向外的电场。一质量为 m 、带电量为＋ q 的粒子，从紧靠内筒且正对狭缝 a 的 s 点出发，初速为零。如果该粒子经过一段时间的运动之后恰好又回到出发点 S ，则两电极之间的电压 U 应是多少？（不计重力，整个装置在真空中）。

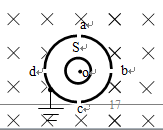
解析 ：如图所示，带电粒子从S出发，在两筒之间的电场力作用下加速，沿径向穿出a而进入磁场区，在洛仑兹力作用下做匀速圆周运动。粒子再回到S点的条件是能沿径向穿过狭缝d。只要穿过了d，粒子就会在电场力作用下先减速，再反向加速，经d重新进入磁场区。然后，粒子将以同样方式经过c、d，再经过a回到s点。

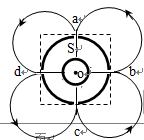
设粒子射入磁场区的速度为V，根据能量守恒，有 ½ mv ² ＝qU

设粒子在洛仑兹力作用下做匀速圆周运动的半径为R，由洛仑兹力公式和牛顿定律得 mv ² /R=qvB

由前面分析可知，要回到S点，粒子从a到d必经过3/4圆周。所以半径R必定等于筒的外半径r ₀ ，则v=qBR/m=qBr ₀ /m，U=mv ² /2q=qB ² r ² ₀ /2m。

【例 5 】如图所示为一种获得高能粒子的装置，环形区域内存在垂直纸面向外．大小可调节的均匀磁场，质量为 m ，电量＋ q 的粒子在环中作半径为 R 的圆周运动， A 、 B 为两块中心开有小孔的极板，原来电势都为零，每当粒子飞经 A 板时， A 板电势升高为 U ， B 板电势仍保持为零，粒子在两板间电场中得到加速，每当粒子离开 B 板时， A 板电势又降为零，粒子在电场一次次加速下动能不断增大，而绕行半径不变．

（ l ）设 t=0 时粒子静止在 A 板小孔处，在电场作用下加速，并绕行第一圈，求粒子绕行 n 圈回到 A 板时获得的总动能 E _n ．

（ 2 ）为使粒子始终保持在半径为 R 的圆轨道上运动，磁场必须周期性递增，求粒子绕行第 n 圈时的磁感应强度 B _n ．

（ 3 ）求粒子绕行 n 圈所需的总时间 t _n （设极板间距远小于 R ）．

（ 4 ）在（ 2 ）图中画出 A 板电势 U 与时间 t 的关系（从 t ＝ 0 起画到粒子第四次离开 B 板时即可）．

（ 5 ）在粒子绕行的整个过程中， A 板电势是否可始终保持为＋ U ？为什么？

解析:

（1）E _n =nqv

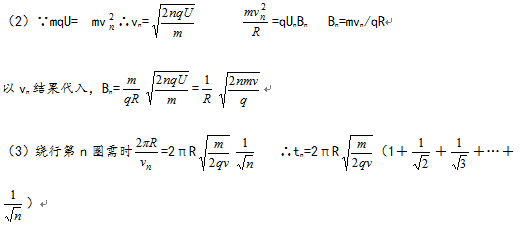
（4）如图所示，（对图的要求：越来越近的等幅脉冲）

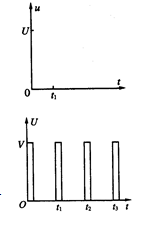
（5）不可以，因为这样粒子在是、B之间飞行时电场对其做功＋qv，使之加速，在是、B之外飞行时电场又对其做功－qv使之减速，粒子绕行一周，电场对其作的总功为零，能量不会增大。

2 、带电粒子在叠加场中的运动

【例6】如图所示，从正离子源发射的正离子经加速电压U加速后进入相互垂直的匀强电场E（方向竖直向上）和匀强磁场B（方向垂直于纸面向外）中，发现离子向上偏转，要使此离子沿直线穿过电场?

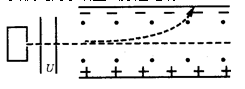
A．增大电场强度E，减小磁感强度B

B．减小加速电压U，增大电场强度E

C．适当地加大加速电压U

D ．适当地减小电场强度E

解析：正离子进入相互垂直的匀强电场和匀强磁场的区域中，受到的电场力F＝qE，方向向上，受到的洛仑兹力f＝qVB，方向向下，离子向上偏，说明了电场力大于洛仑兹力，要使离子沿直线运动，则只有使洛仑兹力磁大或电场力减小，增大洛仑兹力的途径是增大加速电场的电压U或或增大磁感强度B，减小电场力的途径是减小场强E．对照选项的内容可知C、D正确．?

点评：带电粒子进入相互垂直的匀强电场和匀强磁场区域，则它的速度V=E／B，这个区域就是速度选择器，且速度选择器对进入该区域的粒子所带电荷的符号无关，只要是具有相同的速度的带电粒子均能沿直线通过这一区域，但是有一点必须明确的是：速度选择器的进口与出口的位置不具有互换性。

请到「今天看啥」查看全文