正文
然而也正是这一推论导致了以太的终结。它起源于迈克尔逊(Albert Michelson)和莫雷(Edward Morley),完成于爱因斯坦。从1881年开始,迈克尔逊和莫雷等人在不同的时间和地点反复测量了光速,而测量得到的光速在误差范围内总是一样的,并不随地球的运动而变化。这一结果暗示以太可能并不存在
[2]
。1905年,在《论动体的电动力学》(
Zur Elektrodynamik bewegter Körper
)这篇论文中,爱因斯坦首次彻底抛弃了以太的概念,直接提出光速不变原理,建立了狭义相对论。狭义相对论以最简单的方式解释了迈克尔逊-莫雷实验,并给出了横向多普勒效应(transverse Doppler effect)、高速运动粒子的半衰期延长等诸多理论预言。随着这些预言在实验上被逐一验证,人们相信狭义相对论是正确的——以太并不存在。
所以看来真空中确实什么都没有,就像它的名字里暗示的那样是“真正的虚空”?答案并不是这么简单。就像迈克尔逊-莫雷实验对“真空中存在绝对静止的以太”这一说法提出了挑战一样,量子理论的建立对“真空中什么都没有”这一看法也提出了挑战。
原子谱线:“真空” 可能不“空”

氢原子的巴尔末谱线(来源:[b])
证据来源于对原子谱线的观察。早在19世纪,人们就已经发现加高电压的气体可以发光。气体原子通过高电压获得了能量,再通过发光的方式释放能量。这就是霓虹灯的基本原理。不同原子发射的光颜色不同,这些特定频率的光构成了原子的发射光谱
[3]
。氢原子作为元素周期表中最简单的原子,仅由一个质子和一个电子构成,其光谱被研究得最为广泛。氢原子在可见光范围内谱线的频率最早由巴尔末(Johann Balmer)于1885年用一个经验公式总结:
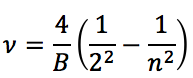
但当时的人们并不知道这公式背后的物理意义。直到1913年,玻尔模型首次成功解释了这一公式(如果你不熟悉玻尔模型,请参考注释[4])。但玻尔模型是一个半经典理论,面临着各种困难。1926年,薛定谔(Erwin Schrödinger)提出薛定谔方程,从完全量子力学的角度解释了氢原子的光谱。电子受吸引的库仑力被束缚在质子附近,处于“束缚态”
(bound state)
。这些束缚态具有确定而分立的能量,被称作能级(energy level)。通过求解薛定谔方程,可以准确预言这些能级的能量。巴尔末公式所总结的处于可见光区的谱线的频率,就对应着处于高能级的电子向第二能级跃迁时所放出的光的频率。
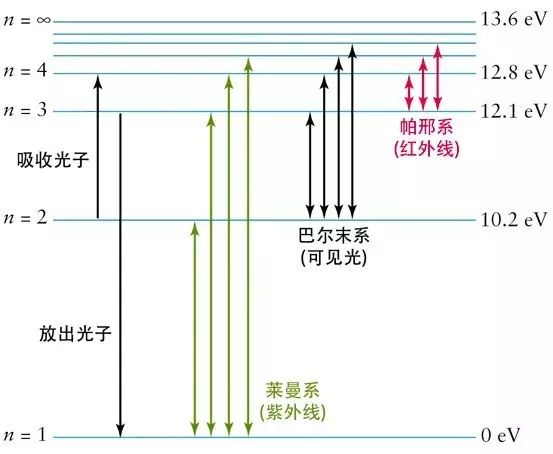
氢原子的能级。改编自:[c]
对氢原子谱线的解释是量子力学的巨大成功。但仔细考察实验结果,我们还是能发现诸多薛定谔方程无法被解释的瑕疵:
• 薛定谔方程只能复制玻尔模型的结果,却不能解释氢原子能级中更精细的结构。如果用更精密的实验放大观察之前得到的谱线,会发现每条谱线实际上都由很多间距很小的谱线所组成。
• 在薛定谔方程的理论框架下,处于能级上的电子无论能量多高,如果不受外界扰动就会一直停留在该能级上,并不会自发跃迁到更低的能级放出光子。但在实验中,即便在真空中,处于高能级的电子仍然会以一定概率跃迁到低能级上。这一现象被称为原子的自发辐射(spontaneous radiation)。
难道真空中真的会有一些东西扰动处于高能级的电子吗?在接下来的两节我们会分别解决这两个问题。但对于处在20世纪20年代的物理学家们而言,这确实是难以理解的现象。物理学家费曼(Richard Feynman)曾经说过这样一个故事
[d]
:
我去过麻省理工学院(读本科),去过普林斯顿大学(读博士)。回到家之后,我的父亲说:“长期以来我一直想搞明白一件事,但一直没搞懂。儿子,既然你已经接受了这么多科学教育,我希望你能解释给我听。”我说好。
他说:“他们说,当原子从一个状态变到另一个状态的时候,从一个激发态变到低能态的时候,会发光。这件事我能明白。”
我说:“确实是这样的。”
“然后,光是一种粒子。他们应该是称之为光子。”
“是的。”
“既然原子从激发态到低能态时出一个光子,那么处于激发态的原子里一定有一个光子了?”
我说:“呃,并不是这样。”
他说:“既然如此,那你是怎么理解这件事情的。一个光子原先并不在原子里面,但原子还是能释放一个光子?”
我思考了几分钟,然后说:“对不起。我不知道。我没法向你解释这件事情。”
我的父亲非常失望。我接受了这么多年的教育,结果竟然是这样糟糕。
狄拉克:真空即是电子海
第一个成功考虑相对论效应,解释了原子光谱中的精细结构(fine structure)的人是狄拉克(Paul Dirac)。1928年,他提出了薛定谔方程的相对论版本来描述电子的运动:

这个方程被称为狄拉克方程。更为重要的是,这个方程以一种石破天惊的方式预言了正电子的存在,并暗示真空中可能有着丰富的物理现象。1933年,薛定谔和狄拉克因为两个以他们名字命名的方程共享了当年的诺贝尔物理学奖。
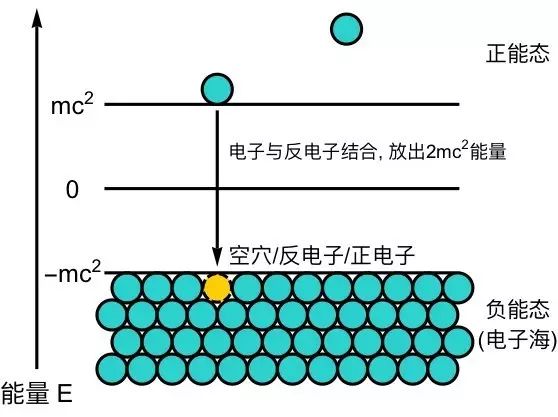
狄拉克电子海中电子和空穴结合的示意图(来源:作者自绘)
狄拉克发现这个方程的解总是成对存在。每一个能量为E的量子态,一定对应着一个能量为-E的量子态。理论上说,一个电子总是可以释放无穷多的能量到达E = -∞的状态,这显然是十分荒谬的。在现实世界中,我们从来没有观测到任何一个电子辐射出无穷多的能量。为了解决这一疑难
[5]
,狄拉克提出了一个天才的解释:电子服从泡利不相容原理(Pauli exclusion principle),即不能有两个电子同时占据一个量子态。如果所有负能态都已经被电子完全占据了,那么泡利不相容原理就可以阻止处于正能态的电子进入负能态。因此在狄拉克的理论中,真空并不是什么都没有,而是充满了负能态电子的电子海洋!
这个理论最大的成功之处在于它准确预言了正电子的存在:如果由于某些原因,一个能量为-|E| 的电子离开了负能电子海,在电子海中留下了一个空穴。那么一个能量为 |E| 的正能态电子将会填上这个空穴,并释放能量 2|E|,使系统重新回到真空:电子(负电荷,|E|) + 空穴 = 真空(电中性) + 2|E|。如此看来,空穴等效地拥有一个正电荷以及正能量。这个空穴就是所谓正电子,它是电子的反粒子。1932年,实验物理学家安德森(Carl Anderson)就在云室里发现了正电子的踪迹。他也因此获得1936年的诺贝尔物理学奖。














