python数据分析之股票实战

正文

请到「今天看啥」查看全文

瞧瞧效果

1	AAPL[ 10 : 15 ]

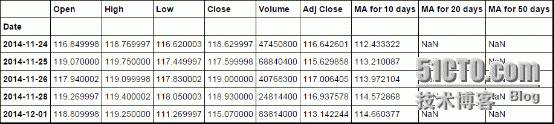
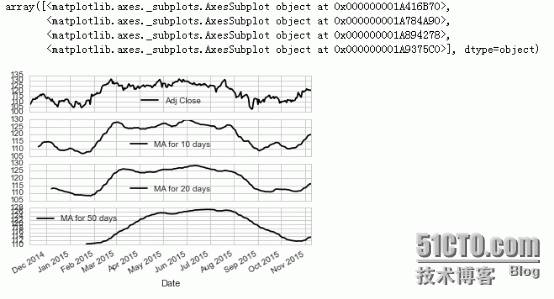
默认subplots这个参数是False的，这里我们瞧瞧True的情况

1	AAPL[[ "Adj Close" , "MA for 10 days" , "MA for 20 days" , "MA for 50 days" ]].plot(subplots = True )

1	AAPL[[ "Adj Close" , "MA for 10 days" , "MA for 20 days" , "MA for 50 days" ]].plot(figsize = ( 10 , 4 ))

很好看有没有!!!

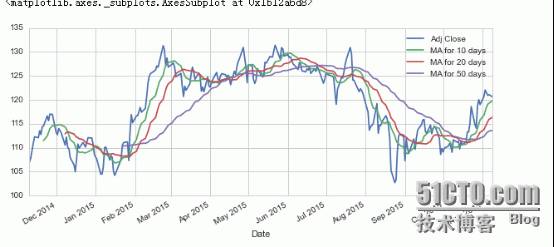
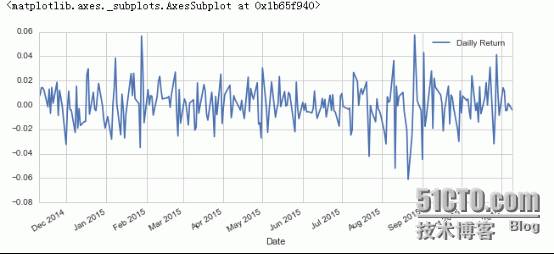
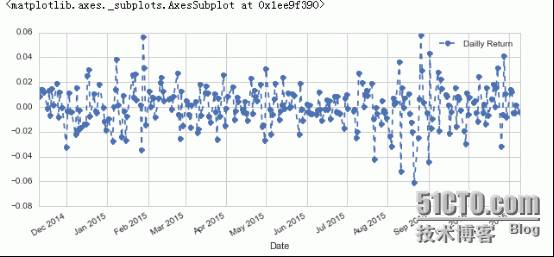
让我们新建一个字段叫做“Dailly Return”,注意Dailly其实我写错了，Dailly Return其实是每日较于前一日的涨幅率.

1 2 3

AAPL[ "Dailly Return" ] = AAPL[ "Adj Close" ].pct_change() ###plot一下 AAPL[ "Dailly Return" ].plot(figsize = ( 10 , 4 ),legend = True )

1 2	###这里我们改变一下线条的类型(linestyle)以及加一些标记(marker) AAPL[ "Dailly Return" ].plot(figsize = ( 10 , 4 ),legend = True ,linestyle = "--" ,marker = "o" )

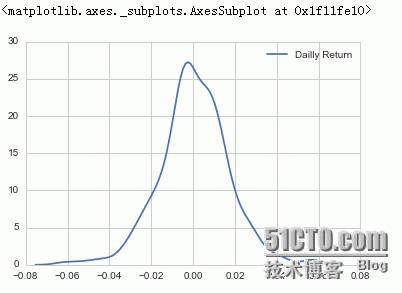
1 2	###再来瞧瞧核密度评估图吧，这里吧Nan指给drop掉 sns.kdeplot(AAPL[ "Dailly Return" ].dropna())

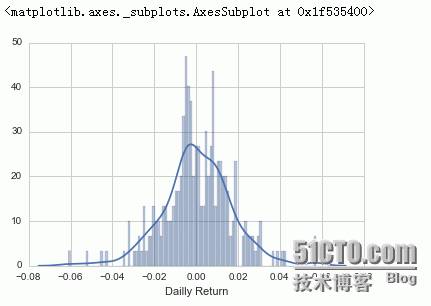
注：This function combines the matplotlib hist function (with automatic calculation of a good default bin size) with the seaborn kdeplot() and rugplot() functions.

由官方说明可知，displot函数是由直方图与seaborn的核密度图以及rugplot（ Plot datapoints in an array as sticks on an axis. ）组合

1 2	###plot一下 sns.distplot(AAPL[ "Dailly Return" ].dropna(),bins = 100 )

1 2 3

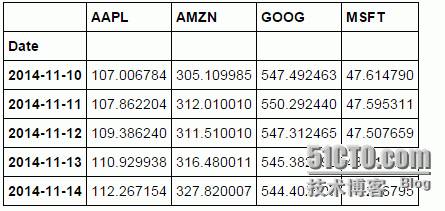
###再来单独获取一下每个公司的调整收盘价记录 closing_df = DataReader(stock_lis, "yahoo" ,start,end)[ "Adj Close" ] closing_df.head()

1 2 3

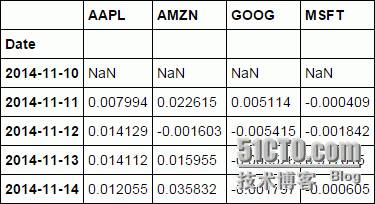
###将每个公司的每日收盘价的百分数变化，及涨幅或者降幅，通过这个我们可以评估它的涨幅前景 tech_rets = closing_df.pct_change() tech_rets.head()

1 2	###平均值都是大于0的，不错 tech_rets.mean(）

AAPL    0.000456

AMZN    0.003203

GOOG    0.001282

MSFT    0.000623

dtype: float64

我们来瞧瞧jointplot这个函数，通过这个函数我们可以画出两个公司的”相关性系数“，或者说皮尔森相关系数（http://baike.baidu.com/view/3028699.htm），如下图所示

如果你看过《大数据时代》这本书，你就会知道为什么作者会求两个公司的相关性了，书中有提到的一个观点是，在大数据时代的到来，我们可以通过大数据来描绘事物之间的相关性并预测，而为什么，是后面要研究的事，注重相关性而不是因果关系。（个人读后感，如有偏驳还望指正）

下面这一部分主要在说相关性~

1	sns.jointplot( "GOOG" , "GOOG" ,tech_rets,kind = "hex" )

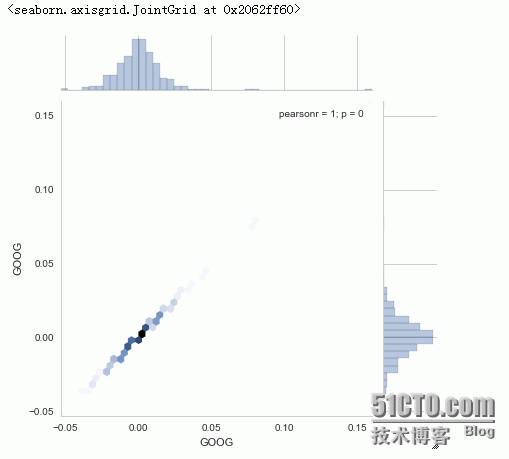
如上图所示，我们画出的事google与google自己的皮尔森相关系数，当然是1啦！值得说明的皮尔森相关系数的值在-1到1之间，1代表正相关，-1代表负相关，0代表没有任何相关性，有兴趣了解怎么算的，参考：https://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient

1	sns.jointplot( "GOOG" , "GOOG" ,tech_rets,kind = "scatter" )

请到「今天看啥」查看全文