正文
33567
0.43
Premium D SI1
60.1
58
830
4.89
4.93
2.95
32864
0.32
Ideal D VS2
61.5
55
808
4.43
4.45
2.73
33624
0.33
Ideal G SI2
61.7
55
463
4.46
4.48
2.76
46435
0.70
Good H SI1
64.2
58
1771
5.59
5.62
3.60
34536
0.33
Ideal G VVS1
61.8
55
868
4.42
4.45
2.74
> par(mfrow = c(
1
,
2
))
> plot(density(dsmall$carat),main =
"carat变量的正态分布曲线"
)
# 绘制carat变量的正态分布曲线
> plot(density(dsmall$price),main =
"price变量的正态分布曲线"
)
# 绘制price变量的正态分布曲线
> par(mfrow = c(
1
,
1
))
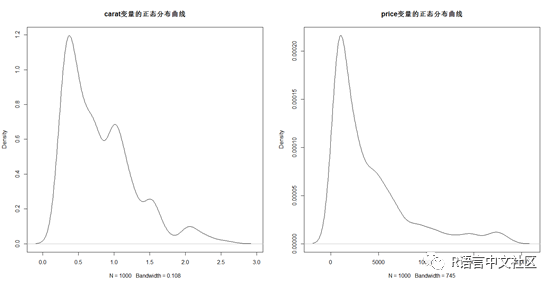
从正态分布图可知,变量carat和price均是严重不对称分布。此时我们利用R语言中的log函数对两者进行对数转换,再次绘制正态密度图。
> par(mfrow = c(1,2))
> plot(density(log(dsmall$carat)),main = "carat变量取对数后的正态分布曲线")
> plot(density(log(dsmall$price)),main = "price变量取对数后的正态分布曲线")
> par(mfrow = c(1,1))

可见,经过对数处理后,两者的正态分布密度曲线就对称很多。最后,让我们一起来验证对原始数据建立线性回归模型与经过对数变量后再建模的区别。
> # 建立线性回归模型
> fit1 # 对原始变量进行建模
> summary(fit1) # 查看模型详细结果
Call:
lm(formula = dsmall$price ~ dsmall$carat, data = dsmall)
Residuals:
Min 1Q Median 3Q Max
-8854.8 -821.9 -42.2 576.0 8234.2
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2391.74 97.44 -24.55 <2e-16 ***
dsmall$carat 7955.35 104.45 76.16 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1582 on 998 degrees of freedom
Multiple R-squared: 0.8532, Adjusted R-squared: 0.8531
F-statistic: 5801 on 1 and 998 DF, p-value: < 2.2e-16
> fit2 lm(log(dsmall$price)~log(dsmall$carat),data=dsmall) # 对两者进行曲对数后再建模
> summary(fit2) # 查看模型结果
Call:
lm(formula = log(dsmall$price) ~ log(dsmall$carat), data = dsmall)
Residuals:
Min 1Q Median 3Q Max
-1.07065 -0.16438 -0.01159 0.16476 0.83140
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.451358 0.009937 850.5 <2e-16 ***
log(dsmall$carat) 1.686009 0.014135 119.3 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2608 on 998 degrees of freedom
Multiple R-squared: 0.9345, Adjusted R-squared: 0.9344
F-statistic: 1.423e+04 on 1 and 998 DF, p-value: < 2.2e-16
通过对比MultipleR-squared发现,模型1的R平方是0.8532,模型2的R平方是0.9345,R平方的值是越接近1说明模型拟合的越好,所以经过对数处理后建立的模型2优于模型1。我们也可以通过在散点图绘制拟合曲线的可视化方式进行查看。
> # 在散点图中 绘制拟合曲线
> par(mfrow=c(1,2))
> plot(dsmall$carat,dsmall$price,
+ main = "未处理的散点图及拟合直线")
> abline(fit1,col="red",lwd=2)
> plot(log(dsmall$carat),log(dsmall$price),
+ main = "取对数后的散点图及拟合直线")
> abline(fit2,col="red",lwd=2)
> par(mfrow=c(1,1))

可见,取对数后绘制的散点更集中在红色的线性回归线上。
分箱转换(Binning)就是把区间型变量 (Interval)转换成次序型变量(Ordinal),其转换的目的如下:
降低变量(主要是指自变量)的复杂性,简化数据。比如,有一组用户的年龄,原始数据是区间型的,从10~60岁,每1岁都是1个年龄段;如果通过分箱转换,每10岁构成1个年龄组,就可以有效简化数据。R语言中有cut函数可以轻易实现数据分箱操作。





