正文
yhat = coefficients[0]
for i in range(len(row)-1):
yhat += coefficients[i + 1] * row[i]
return yhat
我们可以用一个小的数据集对这个函数进行测试。
x, y
1, 1
2, 3
4, 3
3, 2
5, 5
下图是一小部分数据:
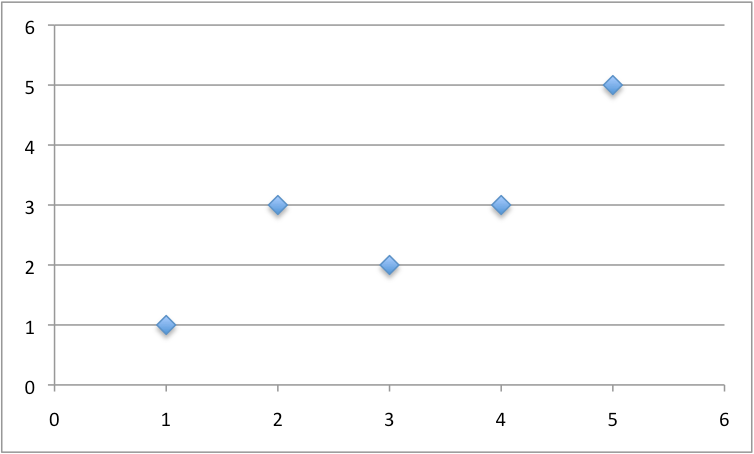
线性回归的部分转换数据
我们也可用之前准备好的系数为这个数据集做预测。predict() 函数测试如下。
# Make a prediction with coefficients
def predict(row, coefficients):
yhat = coefficients[0]
for i in range(len(row)-1):
yhat += coefficients[i + 1] * row[i]
return yhat
dataset = [[1, 1], [2, 3], [4, 3], [3, 2], [5, 5]]
coef = [0.4, 0.8]
for row in dataset:
yhat = predict(row, coef)
print("Expected=%.3f, Predicted=%.3f" % (row[-1], yhat))
单个输入值 (x) 和两个系数(b0 和 b1)。用于建模该问题的预测方程为:
y = b0 + b1 * x
或者,手动选择特定系数:
y = 0.4 + 0.8 * x
运行此函数,我们将得到一个相当接近预测值的输出值(y)。
Expected=1.000, Predicted=1.200
Expected=3.000, Predicted=2.000
Expected=3.000, Predicted=3.600
Expected=2.000, Predicted=2.800
Expected=5.000, Predicted=4.400
现在我们可以用随机梯度下降来优化我们的系数值了。
2. 估计系数
我们可以使用随机梯度下降来为我们的训练数据估计系数值。随机阶梯下降需要两个设定参数:
这两个值和数据集都是函数的参数。我们的这个函数将执行三个遍历循环:
1. 单次 epoch 循环
2. 单次 epoch 中训练集中的每行循环
3. 单次 epoch 中每个系数循环并为每一行更新它
可以看到,每次 epoch,我们都会更新数据集里每行的系数。系数的更新是基于模型生成的误差。该误差被算作候选系数的预测值和预期输出值之间的差。
error = prediction - expected
有一个系数用于加权每一个输入属性,这些属性将以连续的方式进行更新,比如
b1(t+1) = b1(t) - learning_rate * error(t) * x1(t)
列表开始的特殊系数,也被称为截距(intercept)或偏差(bias),也以类似的方式更新,但因其不与特定输入值相关,所以无输入值。
b0(t+1) = b0(t) - learning_rate * error(t)
现在我们把所有东西组合在一起。coefficients_sgd() 函数正是用随机梯度下降来计算一个训练集的系数值,下面即是该函数:
# Estimate linear regression coefficients using stochastic gradient descent
def coefficients_sgd(train, l_rate, n_epoch):
coef = [0.0 for i in range(len(train[0]))]
for epoch in range(n_epoch):
sum_error = 0
for row in train:
yhat = predict(row, coef)
error = yhat - row[-1]
sum_error += error**2
coef[0] = coef[0] - l_rate * error
for i in range(len(row)-1):

















