正文
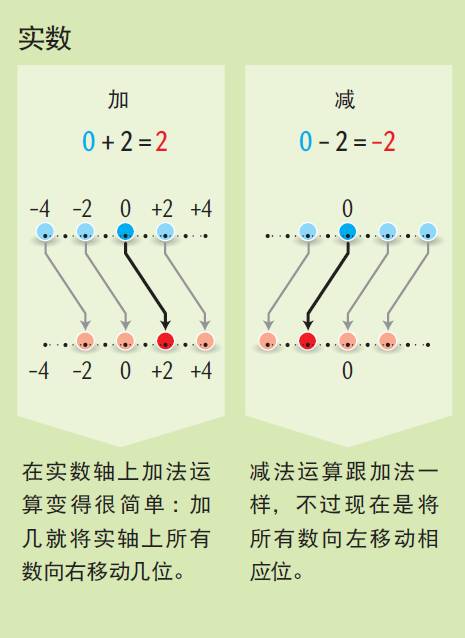
为了理解复数运算和平面几何变换之间的对应关系,我们先用实数来做个热身。实数的加、减运算相当于将代表全体实数的直线
(实轴)
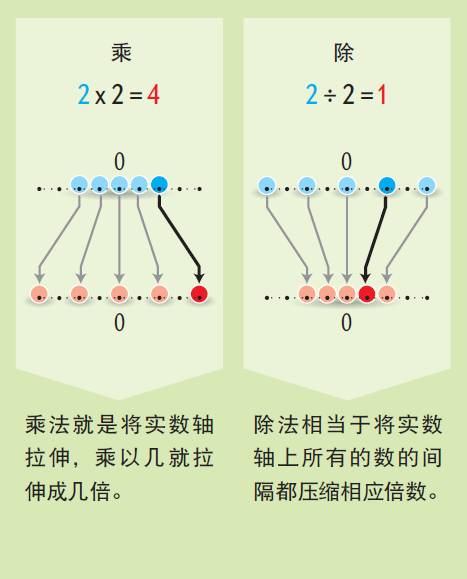
向左或向右移动一定距离。正实数的乘、除则相当于将实轴拉伸或压缩,比如说乘以2及相当于将实轴拉伸2倍,而除以2就是压缩2倍,使得所有点之间的距离都变成此前的1/2。乘以-1相当于将实轴左右调转。
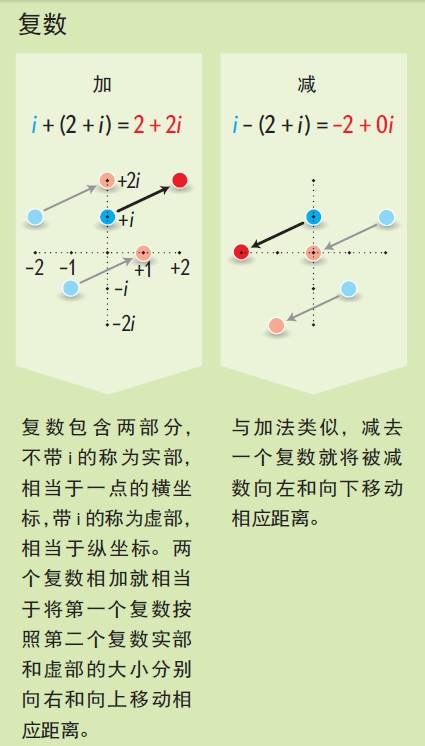
这套规则也适用于复数,只不过稍微多了些花样。给平面上某个点加上一个复数a + bi,就是将该点向左
(或向右,取决于a的正负)
移动a的距离,然后再向上
(或向下,取决于b的正负)
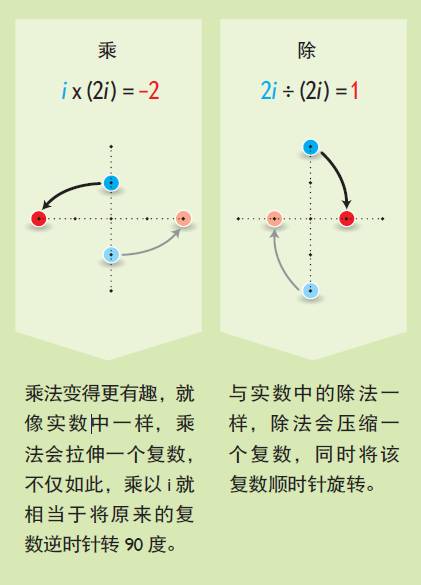
移动b的距离。乘上一个复数则相当于在拉伸或压缩平面的同时旋转整个平面,乘上i意味着将平面逆时针转过90度,所以如果给1乘i再乘i,就相当于将整个平面逆时针转过180度,于是1就变成了-1。复数除法是乘法的逆运算,所以如果乘法拉伸平面除法就压缩平面,反之亦然,然后再反向旋转整个平面。
几乎所有能对实数进行的运算都同样能对复数进行,实际上,很多时候用复数能做得更好,卡丹诺就察觉到了这点,因为用复数我们能解很多用实数无法求解的方程。既然复数这样的二维数系能扩展我们的计算能力,那更高维的数系是不是威力更大呢?很遗憾,当时的数学家没有找到什么简单的手段能继续增加数系的维度,数十年之后,高维数系的秘密方才由一位爱尔兰数学家揭示出冰山一角,而又过了两个世纪,也就是直到今天我们才刚刚开始领教它的强大威力。
1835年,刚过而立之年的数学和物理学家威廉·若万·哈密顿
(William Rowan Hamilton)
发现了如何将一个复数a + bi当作一对实数来处理。当时的数学家普遍采用阿尔冈的方法将复数写成 a + bi的形式,但哈密顿注意到复数可以被看作是两个实数a和b的另一种写法,想通了这一点就可以用一对实数来表示复数,比如a + bi可以记为(a,b)。
这种表示方法的好处是复数的加减运算变得很直观,只须将对应位置上的实数相加减就可以了,比如(a,b)+(c,d)结果就是(a + c,b + d)。哈密顿还找到了该表示中复数乘除法的运算规则,虽然稍微复杂一些,但它保持了阿尔冈所发现的复数漂亮的几何意义。
就这样,哈密顿为对应二维平面几何的复数发明了一套代数运算体系,接着他试图为形如(a,b,c)的三元数组也建立一套这样的代数运算,这样就可以将三维几何与代数联系起来,为此他苦苦追寻多年却劳而无功,后来在给儿子的一封信中他这样回忆那段时光:“每一天早晨,你和你的弟弟威廉·埃德温
(William edwin)
只要一看到我从楼上下来吃早餐,就会问‘爸爸,你会乘三元数了吗?’,而我总是无奈地回答‘不会,我还是只会加减。’”那时的哈密顿还不知道,他给自己设立的目标在数学上是不可能完成的。
哈密顿当时想要寻找的是一个可以进行加、减、乘、除运算的三元数系,这其中除法是最困难的。数学家将可以进行除法运算的数系称为可除代数
(division algebra)
,他们一直对可除代数有一个猜测,但直到1958年才由三位数学家证明这个猜测是个美妙的事实,即只有在一维
(实数)
,二维
(复数)
,四维和八维下才存在可除代数。哈密顿想要成功,除非彻头彻尾地改变数学的规则。
哈密顿的山穷水复在1843年10月16日到来,这一天他与妻子沿着都柏林的皇家运河散步,准备去爱尔兰皇家科学院参加会议,突然之间他灵光一现,要描述三维空间中的转动,仅用三个数是不够的,他还需要第四个数,这样形成一个四维的集合,其中的元素都形如
a + bi + cj + dk
,称为
四元数
(quaternion)
,其中i,j,k表示三个独立的-1的平方根
(即虚数单位)
。
哈密顿后来写到:“彼时彼处,我突然感觉脑海中盘旋的思想电流闭合了,由此激发出来的火花就是i,j,k之间需要满足的等式,这些等式形式是那么完整,我需要做的只是将它们照录下来而已。”接下来他留下了史上最著名的数学家涂鸦,在布鲁厄姆桥
(Brougham Bridge)
的桥墩上刻下了这组等式。今天哈密顿的手刻已经淹没于后人的涂抹之中,取而代之的是一块新立的石板以纪念这次发现。
描述三维空间中的变化竟然需要四维的数组,这看上去也许很怪异,但事实的确如此,描述转动就需要三个数,想象一下飞机如何在三维空间中导航将有助于看清这点,为了保持航向正确,我们需要调节俯仰,也就是机头相对于水平线的上下夹角,接下来需要调节偏航,就像驾驶汽车一样将飞机向左或向右转,最后还需要调节横滚来改变机翼与水平线之间的夹角。与二维平面上类似,三维空间中除了转动同样也有拉伸与压缩,这就需要第四个数来描述。
哈密顿将此后余生都献给了四元数,并发现了很多实际应用,时至今日,很多这类应用中四元数都被更为简单的矢量
(vector)















