物理学咬文嚼字之九十一：线

正文

请到「今天看啥」查看全文

1：1 的距离比，它就没有抛物的意 思，也不含线字。同属圆锥曲线的 双曲线，hyperbola，意思是说过头 了，字面是既没有双字也没有线 字。类似的翻译很多，比如cycloid， 汉译摆线，还有hypocycloid(内摆 线)，epicycloid(外摆线)，其实人家 的字面就是一个cycle 添加了一个另 类的名词性词尾，告诉人们它与圆 有关而已。因为一不关心物理图 像，二不求识其字，数学概念的中 文翻译极为不负责任，贻害匪浅。

关于线和线性的问题，是理解 物理的初步。牛顿第二定律给出质 点运动的方程，接下来玩什么？自 然是如何数学地描述3D 空间中质 点可能的运动轨迹，以及如何求解 特定的力或势场下质点的运动，比 较著名的例子包括catenary( 悬链 线。来自拉丁语catenarius， 链)， brachistochrone(速降线，字面上是 最短时)，isochrones(等时线，字面 上是等时)，等等。这些汉译中的 线字都是额外添加的。再者，功的 定义为 f d s ，这是最简单的微分 1-form，则求沿特定的路径从一点 到另一点所做的功就是线积分(line integral)。在热力学语境中，其主方 程(cardinal equation)是多变量的微 分1-form，即Pfaffian form。类似求 某个循环过程中熵的变化这类问 题，就是线积分。关于线积分的数 学知识教得不充分而去纠缠于某个 过程中系统和环境各自熵变是多少 的问题，无助于对物理学的理解。

若刺激x 和响应y 之间满足关系 y=kx+b，则称此关系是线性的(linear)， 其中y，b 是同类的物理量， 而x 是另一类物理量，k 则反映研究 对象的内禀性质，如在简单的胡克 定理y=kx 中，k 就是物体的弹性系 数；在刚体的定轴转动问题中，k 是转动惯量。在初等解析几何中， y=kx+b 的图像就是一条直线。与线 性关系相映衬的是非线性关系，非 线性(nonlinearity)当然比线性关系复 杂的多，花样也多得多。y=kx ² 这样 的含平方项的关系，算是最简单的 非线性了，它竟然就搪塞了对干涉 现象的解释。除了少数特例，非线 性方程是很难找到严格解析解的。 一个做法是将非线性问题在某些限 制下作线性化(linearization)。对电 磁学问题的线性化导致了有限元算 法从而引发了建筑工程上的革命， 是无心插柳柳成荫的绝佳案例。线 性函数、线性映射的定义是可加性 加上一阶齐次性， 即f(x ₁ + x ₂ ) = f (x ₁ )  + f (x ₂ )  ， f (ax) = af (x) 。如果 是两变量函数具有这样的线性，那 是双线性的(bilinear)。线性关系表 示刺激信号之间没有耦合。一个数 学对象若是能表示成若干个其它数 学对象的线性相加，则称它们是线 性相关的(linearly dependent)。若一 个空间中的矢量，其线性叠加仍是 该空间中的矢量，则该空间是线性 空间。流形的切空间，量子力学中 自伴随算符本征矢量所张的希尔伯 特空间，是我们应该熟知的线性空 间。线性空间的基，是线性无关的 (linearly independent)。

那些有趣的线与非线

3

3.1 射线

Ray，汉译射线，其拉丁语词 源radius ⁷⁾ 本意是车的辐条，从中心 轴出发，向外延展。数学上，ray 被 定义为从一点起始经过另一点无限 延伸所得到的对象。若从一点起始 作一有限的延展，这就是矢量的形 象。Ray，汉译射线，物理上用来 表示从源头向外radiate 的东西，如 rays of light( 光线)， X-ray， γ-ray， cathode ray ( 阴极射线， 即电子)， 等等。Ray 的形象正好反映描述运 动的速度之矢量性质。注意，直线 有矢量定义， 即给定两矢量 a ， b ，参数方程 r = a + λ( b - a ) 描述一 条直线。显然，若λ ∈[0，∞] ，这 定义的是一条射线。

3.2 欧拉线

此例就想说明共线是多么神奇 的事情，它至少是我个人数学教育 中不足的地方。三角形有一些有趣 的心(centers)，比如中心(centroid， 算数平均)， 正心(orthocenter)， 外 心(circumcenter， 外接圆圆心)， Exeter point，以及九点圆的圆心， 都落在一条直线上。这个事实是 1765 年天才的数学家欧拉发现的， 故被称为欧拉线(Euler line； la droite de Euler)。有趣的是， 内心 (incenter，内切圆的圆心)却不在这 条线上。类似地，还有Simson 线， 即对于三角形，其外接圆上任意一 点到三边的三个垂足，是共线的。 这个Simon 线簇的包络， 被称为 Steiner deltoid(三角形)。

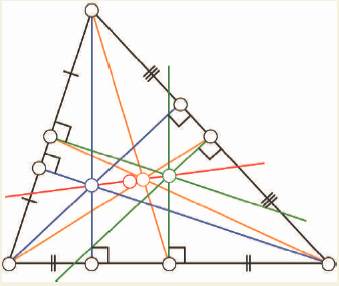
图2 三角形的Euler line，线上的四 点在三角形的内部

3.3 包络线

包络线，envelope，就是英汉 字典里信封那个词。Envelope，动 词形式为envelop，包围、包裹住的 意思。Envelope 常被译成包络线， 这样一来就失去了强调“包络、包 裹”的抽象意义了，二来否认了其 高维推广的存在，不妥。Envelope 也可以是面、体或者更高维的几何 对象，还可以就是包络这个事实， 因此还是简单地译为包络为好。几 何上，对于给定的一个线簇，同线

请到「今天看啥」查看全文