正文
在这个过程中,就需要考虑以上这样做的合适性。
因为只有同个学校学生对自己学校学习氛围打分的情况相近(组内一致性),这样才能用学生的平均分作为学校学习氛围的得分;
相反,如果同个学校的学生对自己学校学习氛围的打分情况有非常大差异,也就是评价两级分化,那么用平均分作为该校的学习氛围得分就不合适了。
Rwg(within-group Interrater ReliabilityCoefficient)系数就是用来评价组内一致性的,也就是评价同一个组内的研究对象在某个问题上的看法是否趋于一致。
Rwg系数有两个,一个是用于单个测量题项的,命名为Rwg(1),另一个是用于多个测量题项的,命名为Rwg(J),它们的计算公式如下:

需要特别说明一下期望分布方差。
表示在特定李克特量表下,组内差异的最大值。
举例说明,加入有10个打分者,它们互相之间没有一点打分一致性,那么可以想象,这10个打分者的打分就是完全随机的,会服从均匀分布。
例如,对于一个5级李克特量表的题目,这10个打分者在完全没有一致性的情况下,它们的打分应该在1,2,3,4,5分数上都有,而且是均值分布的,也就是说,打1分两个人,2分两个人,3分两个人,4分两个人,5分两个人,那么这10个分数的方差等于2。
利用上面的公式计算:
(5^2-1)/12=2,结果也是等于2。
从上方的计算公式可知,Rwg系数没有考虑组间差异,只考虑组内差异。
代表了组内评分者的打分差异,代表不同李克特量表情况下,组内差异的最大值。
那么,用1减去前两者的比值,剩余的部分就可以表示组内一致性情况。
通过上面的讲解可知,每个团体都可以计算一个Rwg值,然后取所有团体Rwg值的平均值或中位数作为整份数据的Rwg值,如果Rwg值达到0.7以上,说明组内一致性较高,那么就可以将每个团体内部调查对象在团体层面得分的平均分作为团体变量的得分,代表团体情况。
例如,上面的学校学习氛围,如果学校内学生对自己学校的学习氛围打分都比较一致,那么就可以用这些学生打分的平均分作为该校的学生氛围得分。
ICC(1)和ICC(2)
上篇文章,草堂君介绍了10种组内相关系数(ICC),在跨层研究中用到的ICC(1)和ICC(2)对应的是10种ICC系数中的ICC(1,1)和ICC(1,k)。
它们都是单个随机因子,区别在于ICC(1)/ICC(1,1)分析的是单次测量数据,而ICC(2)/ICC(1,k)分析的是多测测量的平均值。
具体内容大家可以回顾上篇文章:
通过上面的学习,大家应该知道了,Rwg是用来描述组内一致性的,以此判断是否可以用个人层面收集的团体层面变量的数据平均值来表示团体层面情况,例如上面提高的学校学习氛围的例子。
而ICC1和ICC2称为组内相关系数,测量的是组与组之间的差异性,也就是团体与团体之间的差异性,同样用学校学习氛围这个例子说明,如果学校与学校之间,学习氛围得分存在显著性差异,那么在模型研究中使用学校学习氛围变量,就需要考虑使用跨层模型进行研究。
系数标准及含义

案例分析
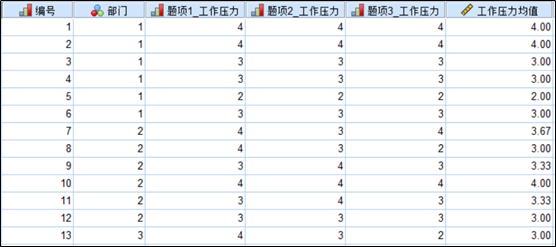
现在有一个测量单位工作压力气氛的量表,总共三个题目。
这份量表总共收回了来自59个单位,每个单位调查6名员工的354份问卷。
数据结果如下所示: