主要观点总结
本文介绍了随机森林算法和决策树的基本概念和构建过程。随机森林是由多个决策树组合而成,用于分类和回归任务。决策树通过树形结构模拟人类决策过程,可以基于给定数据集对新数据进行分类。文章还解释了决策树构建过程中的关键步骤,包括确定根节点、计算Gini impurity、递归决策等,并给出了构建随机森林算法的简单步骤。
关键观点总结
关键观点1: 随机森林和决策树的关系
随机森林是由多个决策树组合而成,用于分类和回归任务。决策树是构建随机森林的基础。
关键观点2: 决策树的基本原理
决策树通过树形结构模拟人类决策过程,可以基于给定数据集对新数据进行分类。
关键观点3: 构建决策树的关键步骤
包括确定根节点、计算Gini impurity、递归决策等,这些步骤用于构建决策树和随机森林。
关键观点4: 随机森林的构建过程
通过集成多个决策树来构建随机森林,可以用于解决复杂的分类和回归问题。
关键观点5: 决策树和随机森林的应用
决策树和随机森林是机器学习中的常用算法,广泛应用于各种分类和回归任务。
正文
"Green" == "Green"))
probility
## Event Probability Type
## 1 Pick Blue, Classify Blue 0.25 TRUE
## 2 Pick Blue, Classify Green 0.25 FALSE
## 3 Pick Green, Classify Blue 0.25 FALSE
## 4 Pick Green, Classify Green 0.25 TRUE
我们再看第二套数据集,10个数据点,2个
red
,3个
blue
,5个
green
。从中随机选一个数据点,再随机选一个分类标签作为这个数据点的标签,分类错误的概率是多少?
0.62
。
probility
"Pick Blue, Classify Green",
"Pick Blue, Classify Red",
"Pick Green, Classify Blue",
"Pick Green, Classify Green",
"Pick Green, Classify Red",
"Pick Red, Classify Blue",
"Pick Red, Classify Green",
"Pick Red, Classify Red"
),
Probability=c(3/10 * 3/10, 3/10 * 5/10, 3/10 * 2/10,
5/10 * 3/10, 5/10 * 5/10, 5/10 * 2/10,
2/10 * 3/10, 2/10 * 5/10, 2/10 * 2/10),
Type=c("Blue" == "Blue",
"Blue" == "Green",
"Blue" == "Red",
"Green" == "Blue",
"Green" == "Green",
"Green" == "Red",
"Red" == "Blue",
"Red" == "Green",
"Red" == "Red"
))
probility
## Event Probability Type
## 1 Pick Blue, Classify Blue 0.09 TRUE
## 2 Pick Blue, Classify Green 0.15 FALSE
## 3 Pick Blue, Classify Red 0.06 FALSE
## 4 Pick Green, Classify Blue 0.15 FALSE
## 5 Pick Green, Classify Green 0.25 TRUE
## 6 Pick Green, Classify Red 0.10 FALSE
## 7 Pick Red, Classify Blue 0.06 FALSE
## 8 Pick Red, Classify Green 0.10 FALSE
## 9 Pick Red, Classify Red 0.04 TRUE
Wrong_probability = sum(probility[!probility$Type,"Probability"])
Wrong_probability
## [1] 0.62
Gini Impurity计算公式:
假如我们的数据点共有
C
个类,
p
(
i
)是从中随机拿到一个类为
i
的数据,
Gini Impurity
计算公式为:
$$ G = \sum_{i=1}^{C} p(i)*(1-p(i)) $$
对第一套数据集,10个数据点,5个
blue
,5个
green
。从中随机选一个数据点,再随机选一个分类标签作为这个数据点的标签,分类错误的概率是多少?错误概率为
0.25+0.25=0.5
。
对第二套数据集,10个数据点,2个
red
,3个
blue
,5个
green
。
从中随机选一个数据点,再随机选一个分类标签作为这个数据点的标签,分类错误的概率是多少?
0.62
。
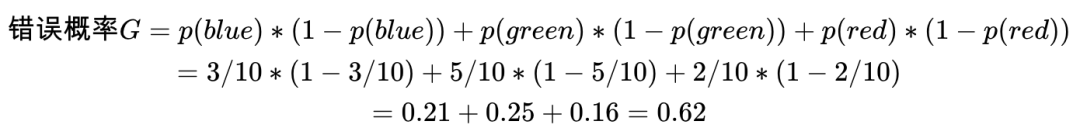
决策树分类后的Gini Impurity
对第一套数据集来讲,按照
x<2
分成两个分支,各个分支都只包含一个分类数据,各自的Gini IMpurity值为0。
这是一个完美的决策树,把
Gini Impurity
为
0.5
的数据集分类为
2
个
Gini Impurity
为
0
的数据集。
Gini Impurity
== 0是能获得的最好的分类结果。
第二套数据集,我们有两种确定根节点的方式,哪一个更优呢?
我们可以先处理变量
x
,选择阈值为
2
,则可获得如下分类:
每个分支的
Gini Impurity
可以如下计算:
当前决策的
Gini impurity
需要对各个分支包含的数据点的比例进行加权,即
我们也可以先处理变量
y
,选择阈值为
2
,则可获得如下分类:
每个分支的
Gini Impurity
可以如下计算:
当前决策的
Gini impurity













