正文
先看一个生活中的例子。
王宏去医院作验血实验,检查他患上了X疾病
(患病比率为千分之一)
的可能性,其结果为阳性。网上的资料显示,实验总是有误差的,这种实验有“百分之一的假阳性率和百分之一的假阴性率”。这句话的意思是说,在得病的人中做实验,有1%的人是假阳性
(即实际是阴性,却得到阳性的结果)
,99%的人是真阳性。而在未得病的人中做实验,有1%的人是假阴性,99%的人是真阴性。于是,王宏根据这种解释,估计他感染X疾病的可能性
(即概率)
为99%。王宏想,既然只有百分之一的假阳性率,那么,百分之九十九都是真阳性,那我感染X病的概率便应该是99%。
可是,医生却告诉他,他被感染的概率只有0.09左右。这是怎么回事呢?王宏的误区在哪里?
医生说:“99%是测试的准确性,不是你得病的概率。你忘了一件事:这种X疾病的患病比率并不大,每千人中只有一个人患X病。”
医生的计算方法是这样的:因为测试的误报率是1%,1000个人将有10个被诊断为假阳性,而根据X病在人口中的比率
(1/1000=0.1%)
,真阳性只有1个。所以,大约11个测试为阳性的人中只有一个是真阳性
(患病)
的,因此,王宏被感染的几率是大约1/11,即0.09
(9%
)
。
实际上,王宏犯了“基本比率谬误”的错误,即忽略了“X病患者在人口中的基本比例为千分之一”这个事实。
谈到基本比率谬误,应先从概率论中著名的贝叶斯定理
[1]
说起。托马斯·贝叶斯
(Thomas Bayes ,1701-1761)
是英国统计学家,贝叶斯定理是他对概率论和统计学作出的最大贡献,是当今人工智能中常用的机器学习之基础框架,它的思想之深刻远出一般人的认知,也许贝叶斯自己生前对此也认识不足。值得一提的是,如此重要的成果却并未在他生前发表,而是在他死后的1763年才由他的朋友发表。本篇将对贝叶斯定理稍作介绍,我们在本系列的后几篇,将讨论贝叶斯学派以及贝叶斯理论在人工智能中的应用。
粗略地说,贝叶斯定理涉及到两个随机变量A和B的相互影响,专业注释为:利用B带来的新信息,应如何修改B不存在时A的“先验概率”P(A),从而得到B存在时的“条件概率”P(A|B)。或者类似地,也可以将A、B反过来叙述,即如何从B的“先验概率”P(B),得到B的“条件概率”P(B|A)。正反两种叙述方式分别对应于下图中的实线和虚线。
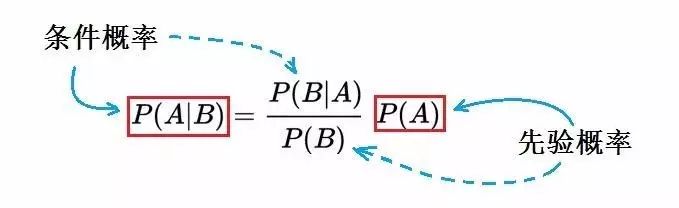
通过前述王宏的经历我们就能很好的理解这个公式:随机变量A表示“王宏感染X病”;随机变量B表示“王宏的检查结果”。先验概率P(A)指的是王宏没有检查结果时得X病的概率
(即X病在公众的基本概率0.1%)
,而条件概率
(或后验概率)
P(A|B)指的是王宏“检查结果为阳性”的条件下得X病的概率
(9%)
。也就是说,王宏的检查结果将先验概率P(A)
( 0.1%)
修正成为9%。
贝叶斯定理是十八世纪的产物,却在二十世纪七十年代遇到了挑战,该挑战来自于卡尼曼和特维尔斯基提出的“基础概率谬误”
(Base Rate Fallacy)
。丹尼尔·卡尼曼
(Daniel Kahneman,1934-)
是以色列裔美国心理学家,2002年诺贝尔经济学奖得主。基础概率谬误并不是否定贝叶斯定理,而是探讨一个使人困惑的问题:为什么人的直觉经常与贝叶斯公式计算的结果相悖?如同刚才的例子所示,人们在使用直觉的时候经常会忽略基础概率。卡尼曼等在他的文章 《思考,快与慢》
(
)
中举了一个出租车的例子来启发人们思考这个影响人们“决策”的原因:
某城市有两种颜色的出租车:蓝和绿
(比率为15:85)
。一辆出租车夜间肇事后逃逸,一位目击者认定肇事的出租车是蓝色的。然而,他“目击的可信度”如何呢?公安人员经过在相同环境下对该目击者进行“蓝绿”测试得出结论:正确识别率为80%,20%的情况不正确。也许有读者立刻就得出了结论:肇事车辆是蓝色的概率应该是80%。如果你作此回答,你便是犯了与前文提到的王宏同样的错误,忽略了先验概率,没有考虑在这个城市中“蓝绿”车的基本比例。
那么,肇事车辆是蓝色的
(条件)
概率应为多少?贝叶斯公式能给出正确的答案。首先我们必须考虑蓝绿出租车的基本比例
(15: 85)
。也就是说,在没有目击证人的情况下,肇事车辆是蓝色的概率只有15%,即“A=蓝车肇事”的先验概率P(A)=15%。现在,一位目击者的出现改变了事件A出现的概率。目击者看到车是“蓝”色的。不过,他的目击能力也要打折扣,只有80%的准确率,即也是一个随机事件
(记为B)
。
我们的目的是要得出在有目击证人“看到蓝车”的条件下肇事车辆“真正是蓝色”的概率,即条件概率P(A|B)。后者应该大于先验概率的15%,因为目击者看到“蓝车”。如何修正先验概率?需要计算P(B|A)和P(B)。
因为A=车为蓝色、B=目击蓝色,所以P(B|A)是在“车为蓝色”的条件下“目击蓝色”的概率,即P(B|A) =80%。最后还要算总概率P(B),它的计算麻烦一点。P(B)指的是“目击证人看到一辆车为蓝色的概率”,等于两种情况的概率相加:一种是车为蓝,辨认也正确;另一种是车为绿,错看成蓝。所以:
P(B) = 15%×80% + 85%×20% = 29%
从贝叶斯公式:
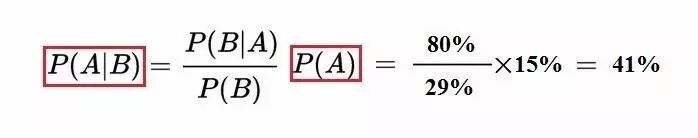
可以算出在有目击证人情况下肇事车辆是蓝色的几率=41%,同时也可求得肇事车辆是绿车的概率为59%。被修正后的“肇事车辆为蓝色”的条件概率41%大于先验概率15%很多,但是仍然小于肇事车为绿的概率0.59。
抛硬币、掷骰子之类游戏中涉及的概率,是离散的,抛丢结果的数目有限
(硬币仅有两种结果,骰子为6种)
。如果硬币或骰子是对称的,每个基本结果发生的概率相等。这种随机事件被称为古典概型。数学家们将古典概型推广到某些几何问题中,使得随机变量的结果变成了连续的、结果数目无限多的概型,这种随机事件被称之为“几何概型”。古典概型向几何概型的推广,类似于有限多个整数向“实数域”的推广。了解几何概型很重要,因为与之相关的“测度” 概念
(长度、面积等)
,是现代概率论的基础。
布丰投针问题,是第一个被研究的几何概型。
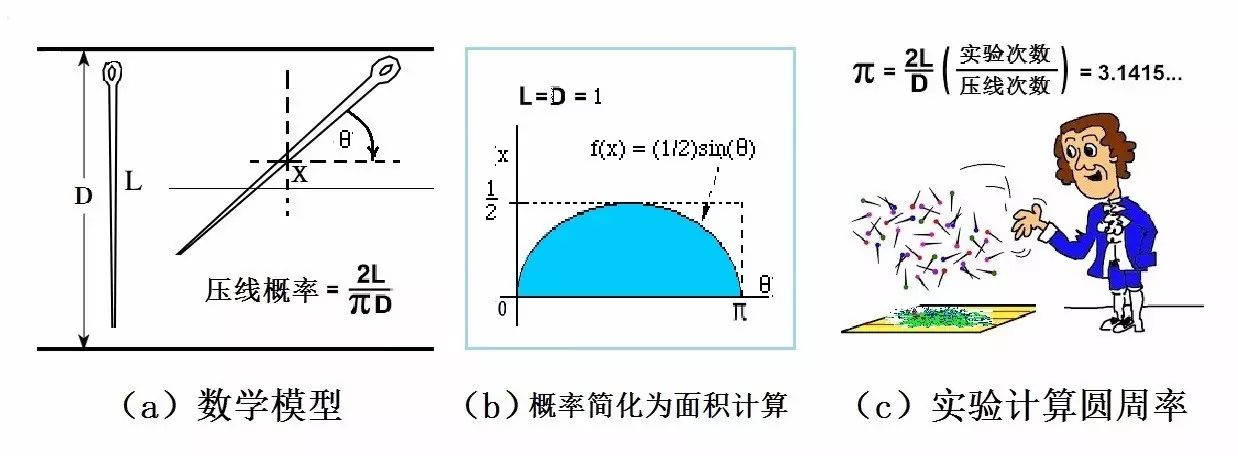
►
图1:布封(Buffon)投针问题





