正文
彭罗斯贴砖吸引大众的原因主要有两个。
其一,是他找到了只用两种贴砖就生成无限变化图案的方式。其二则更了不起,他找到的这两种贴砖,都是形状简单的对称图形,本身看不出一点不寻常的迹象。
彭罗斯为他的非周期贴砖设计了几种不同的版本。最有名的一套称为
“风筝”与“飞镖”
。“风筝”看上去就和孩子们玩的风筝一样,飞镖的轮廓则像简化版的隐形轰炸机。两者都能干净利落地由对称轴一分为二,它们的表面还绘有两条简单、对称的弧线。彭罗斯制定了一条平铺规则:“合法”的拼贴必须能使弧线对接,连成连续的曲线。没有这条规则,风筝和飞镖就会摆出重复的图案;而在这条规则之下,就永远都不会出现重复。风筝和飞镖,永恒地舞动在五条对称轴周围,组合出满天星、十边形,蜿蜒的长线则绘成蝴蝶与花朵的形状。形态似“似”而非,蕴藏无穷变化。

风筝与飞镖:英国数学家罗杰·彭罗斯只用风筝和飞镖两种形状(图中蓝线段构成的图形),就构造出了这片充满美感、变化无穷的图案。
阿肯色大学数学系助理教授埃蒙德·哈里斯(Edmund Harriss)的博士论文主题就是彭罗斯贴砖。他为我们做了一个对比:“试想你走在一个由正方形构成的世界里,你每走到一块正方形的边缘,下一块都还是同样的正方形。一直走下去,你都知道会看到什么东西。”而彭罗斯贴砖的性质正好完全相反。
“不论你掌握了多少信息、看过多少贴砖排列,你都无法预测下一步的花纹,它将会是你之前从未见过的图案。”
平面上的非周期图案具有一个奇特的性质,排布位置的信息似乎能够通过某种方式跨过很大距离进行传递。某处的一块贴砖可以防止数百(甚至数千、数百万)块贴砖之外出现某种排列类型。哈里斯说:“局部约束鬼使神差地拓展为全局约束。这些贴砖在任何尺度下都不会出现周期性的片段。”比如,你可能要选择在一处放一块风筝,或是在另一处放一块飞镖。这两件事都能做到,但无法同时实现。
在这些组合成无穷非重复图案的贴砖中,能看到斐波那契比例的身影。斐波那契比例又称为“黄金比例”。如果在两个数中,较小数与较大数的比,等于较大数与两数之和的比,那么这两个数就符合黄金比例。就贴砖来说,风筝的面积与飞镖的面积比等于黄金比例;风筝的长边与短边之比也等于黄金比例。
彭罗斯贴砖还可以分割成小一号的贴砖。风筝可以分成两片小风筝和两片半块的小飞镖;飞镖可以分成一片小风筝和两片半块的小飞镖。(在任何合理的拼贴方式下,那些半块的飞镖都能两两组合。数学上我们将两片半块飞镖视为一个整体。)哈里斯说:“假设我有一片彭罗斯贴砖,包含 A 块风筝和 B 块飞镖,那么分割一次之后,我就能得到 2A + B 块风筝和 A + B 块飞镖。”
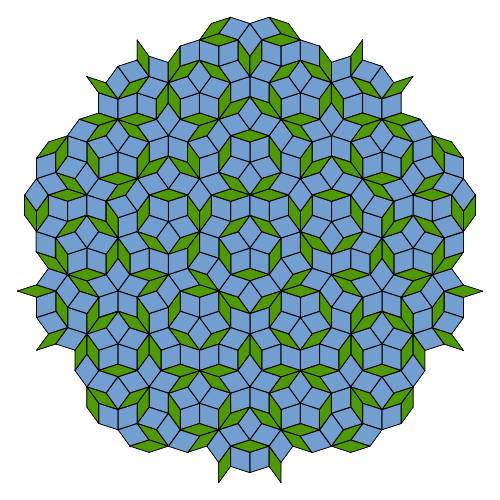
彭罗斯瓷砖的另一种图案。图片来源:维基百科





