学好概率思维（4）——聊聊“大数定律”

概率思维做投资 · 公众号 · · 2017-05-01 21:19

正文

通过中心极限定理，我们也可以理解持续参与正和游戏是一定盈利的。由于正和游戏的期望收益都是正的，那么多次参与正和游戏后，总的期望收益是每一次期望收益之和。多次参与后，这个期望收益会越来越大。但标准差增长的幅度却没有期望收益增长那么快，增长幅度是参与次数的开根号。

因此，随着参与次数的增加，期望收益与标准差之比越来越大。从前面的例子可以看出，参与1000次，期望收益与标准差之比是0.63。而参与10万次，期望收益与标准差之比是6.3。随着参与次数继续增多，这个比率会越来越大。

我们知道，在正态分布情况下，3倍标准差外的事件都是小概率事件，6倍标准差几乎就是不可能发生的事件。所以，随着参与次数的增加，持续参与正和游戏而亏损的可能性就越来越低，到了一定程度就几乎为0了。

同样的，做为赌场老板的对立面，赌徒的命运也是跑不出大数定律和中心极限定理的。

由于赌徒参与的是负和游戏，每一次的期望收益都是负的，所以持续参与，一定能获得他的平均收益，也就是负收益。平均都是负的，参与次数又多，不倾家荡产才怪。

随着赌徒参与次数的增加，他输钱的期望值的绝对值与标准差之比也越来越大，赢钱变成了一件几乎不可能实现的事件，那么亏钱也就几乎是个必然事件了。下表计算了赌场老板持续参与胜率为51%的游戏的结果。

表1 持续参与胜率为51%的游戏的结果

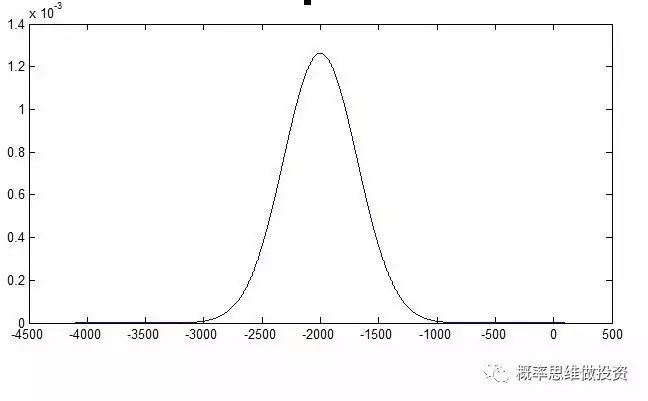
下图是期望收益为-2000，标准差为316的正态分布概率密度函数图。可以看出，发生正收益的可能性几乎为0。

4. 举一反三

从上面的例子和分析可以看出，做投资如果持续参与正和游戏，长期坚持下来，一定是获利的。下面再举几个例子，希望起到抛砖引玉的效果。

1）赌场老板设置赔率不均衡

上面的例子是概率对赌场老板有利，其实赌场老板不光追求概率有利，赔率有利时他也是很高兴的。总之他追求的正和游戏，也就是期望收益为正的游戏。

如果还是猜硬币的游戏，但硬币是均匀的，向上和向下各有50%的可能性。如果赌徒猜对了，赢1块钱；猜错了，输1.1元。那么对于赌徒来说，同样是个期望收益为负的游戏，也就是负和游戏。对赌场老板来说，则是个正和游戏。

澳门或者拉斯维加斯的赌场老板们，购买那些老虎机的时候，早就在程序里设置好了。或者是概率对自己有利，或者是赔率对自己有利，总之是期望收益为正。大量的赌徒持续的参与这样的游戏，保证了赌场老板一定是盈利的。

2）封闭式基金折价套利

我以前反复提到过封闭式基金是个好的投资品种。封闭式基金由于有折价，持有到期后，折价一定会消失的。这个折价消失的过程，对于封闭式基金持有人就是个正和游戏。

持有到期后，大盘有可能涨，有可能跌。姑且认为大盘涨和跌的概率各是50%吧（其实大盘是个长期向上的过程，涨的概率是大于50%的），加上封闭式基金的折价缩小，那么就变成了一个获胜概率超过50%的游戏，即正和游戏。

参与每一次封闭式基金的封转开，都不保证一定是盈利的，但这一定是个正和游戏。长期持续参与这样的游戏，最终的结果一定是盈利的。

3）股指期货吃贴水套利

股指期货在贴水的情况下，其实就相当于封闭式基金折价。股指期货到期交割时，贴水一定会消失的。做多贴水的股指期货，也是不保证每次都盈利，但是个获胜概率大于50%的正和游戏。

4）开放式基金停牌股套利

有些股票被借壳重组或者有重大的利好消息，复牌时往往有若干个连续涨停。这时候瞪眼、眼红、干着急都是买不到的。但如果我们申购重仓这只股票的开放式基金，则可以搭个顺风车，随着基金净值的增长而获利。