正文
前面我们通过自顶向下的方式维护了一个最大堆,这里将通过自底向上的方式通过MAX-HEAPIFY将一个
n=A.length的数组
A[1...n]转换成最大堆。
回顾一下上面的图示,其总共有9个结点,取小于或等于9/2的最大整数为4,从4+1,4+2,一直到n都是该树的叶子结点,你发现了么?这对任意n都是成立的哦。
因此这里我们就要从4开始不断的调用MAX-HEAPIFY(A,i)来构建最大堆。
为什么会有这一思路呢?
原因是既然我们知道了哪些结点是叶子结点,从最后一个非叶子结点(这里是4)开始,一次调用MAX-HEAPIFY函数,就会将该结点与叶子结点做相应的调整,这其实也就是一个递归的过程。
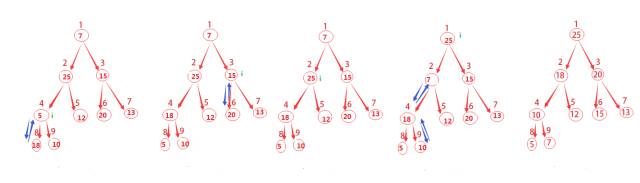
图示已经这么清晰了,就直接上伪代码咯。
BUILD-MAX-HEAP(A)
1 A.heap-size=A.length
2 for i=小于或等于A.length/2的最大整数 downto 1
3 MAX-HEAPIFY(A,i)
通过HEAPSORT进行堆排序算法
所谓的堆排序算法,先通过前面的BUILD-MAX-HEAP将输入数组
A[1...n]建成最大堆,其中
n=A.length。而数组中的元素总在根结点
A[1]中,通过把它与
A[n]进行互换,就能将该元素放到正确的位置。
如何让原来根的子结点仍然是最大堆呢,可以通过从堆中去掉结点n,而这可以通过减少
A.heap−size来间接的完成。但这样一来新的根节点就违背了最大堆的性质,因此仍然需要调用MAX-HEAPIFY(A,1),从而在
A[1...n−1]上构造一个新的最大堆。
通过不断重复这一过程,知道堆的大小从
n−1一直降到2即可。

上图的演进方式主要有两点:
1)将
A[1]和
A[i]互换,
i从
A.length一直递减到2
2)不断调用MAX-HEAPIFY(A,1)对剩余的整个堆进行重新构建
一直到最后堆已经不存在了。
HEAPSORT(A)
1 BUILD-MAX-HEAP(A)
2 for i=A.length downto 2
3 exchange A[1] with A[i]
4 A.heap-size=A.heap-size-1
5 MAX-HEAPIFY(A,1)
优先队列
下一篇博文我们就会介绍大名鼎鼎的快排,快速排序啦,欢迎童鞋们预定哦~
话说堆排序虽然性能上不及快速排序,但作为一个尽心尽力的数据结构而言,其可谓业界良心呐。它还为我们提供了传说中的“优先队列”。
优先队列(priority queue)和堆一样,堆有最大堆和最小堆,优先队列也有最大优先队列和最小优先队列。
优先队列是一种用来维护由一组元素构成的集合S的数据结构,其中每个元素都有一个相关的值,称之为关键字(key)。
一个最大优先队列支持一下操作:
MAXIMUM(S):返回
S中有着最大键值的元素。
EXTRACT−MAX(S):去掉并返回
S中的具有最大键字的元素。
INCREASE−KEY(S,x,a):将元素
x的关键字值增加到
a,这里假设
a的值不小于
x的原关键字值。
INSERT(S,x):将元素
x插入集合
S中,这一操作等价于
S=S∪{x}。
这里来举一个最大优先队列的示例,我曾在关于“50% CPU 占有率”题目的内容扩展 这篇博文中简单介绍过Windows的系统进程机制。
这里以图片的形式简单的贴出来如下:

在用堆实现优先队列时,需要在堆中的每个元素里存储对应对象的句柄(handle)。句柄的准确含义依赖于具体的应用程序,可以是指针,也可以是整型数。
在堆的操作过程中,元素会改变其在数组中的位置,因此在具体实现中,在重新确定堆元素位置时,就自然而然地需要改变其在数组中的位置。
一、前面的
MAXIMUM(S)过程其实很简单,完全可以在
Θ(1)时间内完成,因为只需要返回数组的第一个元素就可以呀,它已经是最大优先队列了嘛。





