正文
神经网络具有拟合非线性函数的能力。但是为了拟合不同的非线性函数,我们是否需要设计不同的非线性激活函数和网络结构呢?
答案是不需要。
universal approximation theorem
已经证明,前向神经网络是一个通用的近似框架。 简单来说,对常用的 sigmoid,relu 等激活函数,即使只有一层隐藏层的神经网络,只要有足够多的神经元,就可以无限逼近任何连续函数。在实际中,浅层神经网络要逼近复杂非线性函数需要的神经元可能会过多,从而提升了学习的难度并影响泛化性能。因此,我们往往通过使用更深的模型,从而减少所需神经元的数量,提升网络的泛化能力。
深度神经网络是深度学习中的一类算法,而深度学习是机器学习的一种特例。因此,这一节我们在机器学习的一般框架下,介绍模型训练相关的基本概念,及其在 Tensorflow 中的实现。相关概念适用于包括 NN 在内的机器学习算法。
常见的机器学习问题,可以抽象为 4 大类问题:
根据训练数据是否有 label,可以将问题分为监督学习(所有数据都有 label),半监督学习(部分数据有 label)和非监督学习(所有数据都没有 label)。 增强学习不同于前 3 种问题,增强学习也会对行为给出反馈(reward),但关注的是如何在环境中采取一系列行为,从而获得最大的累积回报。监督学习是目前应用最广泛,也是研究最充分的机器学习问题,本文接下来将重点介绍监督学习。
在监督学习中,给定 N 个训练样本

我们的目标是得到一个从输入到输出的函数:

实际中,我们通常不会直接优化函数 f,而是根据问题的具体情况,选择一组参数化的函数 fθ, 将优化函数 f 转换成优化参数θ。
常见的分类问题和回归问题,都是监督学习的一种特例。线性分类器,深度神经网络等模型,都是为了解决这些问题设计的参数化后的函数。为了简单,我们以线性分类器

为例,需要优化的参数θ为 (w,b)。
为了衡量函数的好坏,我们需要一个客观的标准。 在监督学习中,这个评判标准通常是一个损失函数

对一个训练样本
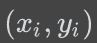
模型的预测结果为 y^,那对应的损失为

损失越小,表明函数预测的结果越准确。实际中,需要根据问题的特点,选择不同的损失函数。
二分类问题中,常用的 logistic regression 采用 sigmoid + cross entroy 作为 loss。对常见的 loss,tensorflow 都提供了相应的函数。
loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=labels, logits=y)

对多分类问题,如上图所示,我们可以将二分类的线性分类器进行扩展为 N 个线性方程:
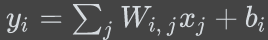
然后通过





