正文
1
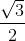
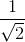
0
tan
0
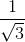
1
★
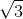
表中的星号表示 tan (π/2) 无定义. 事实上, 正切函数在 π/2 处有一条垂直渐近线 (从图像上看会很清楚, 我们将在 2.3 节对此进行研究). 无论如何, 你必须能够熟练地说出该表中的任意一项, 而且来回都要掌握! 这意味着你必须能够回答两类问题. 这两类问题的例子是：
(1) sin (π/3) 是什么？(使用该表, 答案是
. )
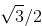(2) 介于 0 到 π/2, 其正弦值为
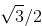的角是什么？(显然, 答案是 π/3. )
当然, 你必须能够回答该表中的每一项所对应的这两类问题. 就算我求大家了, 请背熟这张表! 数学不是死记硬背, 但有些内容是值得记忆的, 而这张表一定位列其中. 因此, 无论是制作记忆卡片, 让你的朋友来测验你, 还是每天抽一分钟记忆, 不管用什么办法, 请背熟这张表.
2.2 扩展三角函数定义域
上表 (你背熟了吗？) 仅仅包括介于 0 到 π/2 的一些角. 但事实上, 我们可以取任意角的正弦或者余弦, 哪怕这个角是负的. 对于正切函数, 我们则不得不小心些. 例如, 上面我们看到的 tan (π/2) 是无定义的. 尽管如此, 我们还是能够对几乎每一个角取正切.
让我们首先来看看介于 0 到 2π (记住, 2π 就是 360°) 的角吧. 假设你想要计算 sin (
θ
) (或 cos (
θ
) 或 tan (
θ
)), 其中
θ
是介于 0 到 π/2 的角. 为了看得更清楚, 我们先来画一个带有一点古怪标记的坐标平面, 如图 2-5 所示.
注意到坐标轴将平面分成了四个象限, 标记为Ⅰ到Ⅳ, 且标记的走向为逆时针方向. 这些象限分别被称为第一象限、第二象限、第三象限和第四象限. 下一步是要画一条始于原点的射线 (就是半直线). 那么究竟是哪一条射线呢？这取决于角
θ
. 来想象一下, 你自己站在原点上, 面向
x
轴的正半轴. 现在沿着逆时针方向转动角
θ
, 然后你沿着一条直线向前走. 你的足迹就是你要找的那条射线了.
现在, 图 2-5 (以及图 2-2) 中的其他标记就说得通了. 事实上, 如果你转动了角 π/2, 你将正面向上并且你的足迹将是
y
轴的正半轴. 如果你转动了角 π, 你将得到
x
轴的负半轴. 如果你转动了角 3π/2, 你将得到
y
轴的负半轴. 最后, 如果你转动了角 2π, 那么就又会回到了你起始的那个位置, 即面向
x
轴的正半轴. 这就好像你根本没转动过! 这就是为什么图中会有 0 ≡ 2π. 对于角度而言, 0 和 2π 是等价的.
好了, 让我们取某个角
θ
并以恰当的方式画出它. 或许它就在第三象限的某个地方, 如图 2-6 所示.
注意到我们将这条射线标记为
θ
, 而不是这个角本身. 不管怎样, 现在在这条射线上选取某个点并从该点画一条垂线至
x
轴. 我们对三个量感兴趣：该点的
x
坐标和
y
坐标 (当然它们被称为
x
和
y
), 以及该点到原点的距离, 我们称为
r
. 注意,
x
和
y
可能会同时为负 (事实上, 在图 2-7 中它们均为负). 然而,
r
总是正的, 因为它是距离. 事实上, 根据毕达哥拉斯定理 (即勾股定理), 不管
x
和
y
是正还是负, 我们总会有
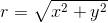. (平方会消除任何负号.)
有了这三个量, 我们就可以定义如下的三个三角函数了：
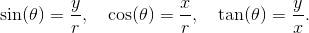
将量
x
、
y
和
r
分别解释为邻边、对边和斜边, 这些函数恰好就是 2.1 节中的固定公式了. 不过等一下, 如果你在那条射线上选取了另外一个点, 那会是什么样子呢？ 这不要紧, 因为你得到的新的三角形和原来的那个三角形是相似的, 而上述比值不会受到任何影响. 事实上, 为方便起见, 我们常常假设
r
= 1, 这样得到的点 (
x
,
y
) 会落在所谓的
单位圆
(就是以原点为中心, 半径为 1 的圆) 上.
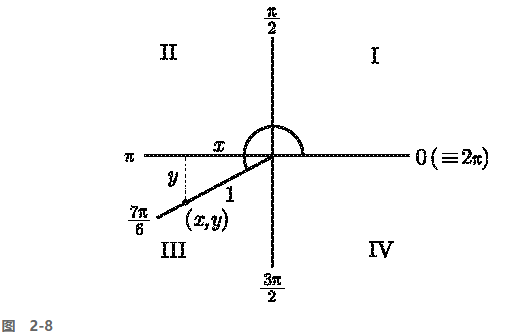
现在来看一个例子. 假设, 我们想求 sin (7π/6). 首先, 7π/6 会在第几象限呢？ 我们需要决定 7π/6 会出现在列表 0, π/2, π, 3π/2, 2π 的哪个地方. 事实上, 7/6 大于 1 但小于 3/2, 故 7π/6 在 π 和 3π/2 之间. 事实上, 图 2-8 看起来很像前面的例子.
