正文
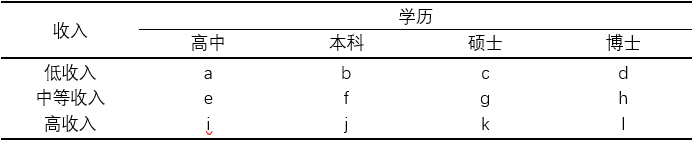
如上表所示,两个定序型变量的水平排列都是由低水平到高水平的,具有单调性,那么水平组合之间就有一致对和非一致对的区别。例如,水平组合a和水平组合f,af就是一致对,因为符合学历增加,收入提高的单调性(a是低收入和高中,f是中等收入和本科);而水平组合d和水平组合e,de就是非一致对,是反单调性的(d是低收入和博士,e是中等收入和高中)。
还有两种对子情况,行对和列对。例如,ab(行对)和ae(列对),在ab这个对子中,它们的行变量水平都是相同的,为低收入,因此称为行对,而ae的列变量水平是相同的,为高中,称为列对。
通过以上的对子情况介绍,大家可以指导,列联表的水平组合对子可以分为一致对、非一致对、行对和列对。我们将它们都列出来,如下所示:

由上表可知,总的水平组合对数为18+18+18+16=66,总对数也可以用排列组合公式得出:
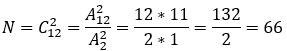
对于两个定序型变量的相关系数,需要用到以上一致对、非一致对、行对、列对和总对数之间的比例关系。很好理解,可以想到一致对越多,正相关关系越强,非一致对的比例越高,负相关关系越强。下面我们介绍的Gamma、tau-b、tau-c和Somers‘d系数都是基于以上对子情况而建立的相关系数。
Gamma系数
Gamma系数也被称为Goodman andKruskal‘s gamma系数。Gamma系数适用于两个定序型变量的相关性分析,它的计算公式如下:
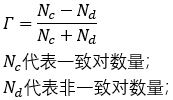
从Gamma的公式可知,如果两个定序型变量的所有数值对都是一致对,那么Gamma的值为+1,反之则为-1。Gamma相关系数没有考虑秩次相同的数值对(行对和列对)。
tau相关系数
tau相关系数又被称为Kendall tau相关系数,有三种类型:Kendall‘s tau-a; Kendall’s tau-b; Kendall’stau-c,在SPSS的两变量相关分析菜单和大多数的统计书籍中,介绍的Kendall相关系数是Kendall tau-b相关系数。三种Kendall相关系数的计算公式如下:

tau-a不常用,tau-b常用于两个定序型变量且水平数相同的情况;而tau-c适用于两个定序型变量但水平数不同的情况,此外,因为tau-c在分母只考虑变量的低水平数,所以tau-c也适用于因变量为定序,自变量为定类的情况。在SPSS中,可以计算Kendall‘s tau-b和Kendall’s tau-c。





