正文
1611年,伟大的天文物理学家约翰尼斯·开普勒(Johannes Kepler)的妻子去世,两年后,科学家准备续弦,重新组建家庭。
天文物理学家择偶,过程自然是非常硬核。由于开普勒的上一段婚姻并不幸福,所以这次他拿出研究天文学的精神,列出多项参数,对交往的女士详细考察,力求找到完美的对象,其严谨程度不亚于在太空中寻找一颗小行星。

开普勒像面试一样挨个交往相亲对象,在见到第5名女性时,他眼前一亮,被对方的勤俭持家、善良忠诚所打动,本想就此收手,但毕竟男人都是大猪蹄子,“下一个是不是更棒?”的想法,驱使他继续去情场猎艳。
最后,开普勒一共交往了11名女士,但他并没有找到更好的,反而一直对第5名女士牵肠挂肚。在某天去演讲的途中,他突然下定决心,调头前往第5名女士的家里,厚着脸皮向这位被他拒绝过的女士求婚。幸运的是,对方答应了。
就这样,开普勒跟这名叫做苏珊·罗伊特林格的女子结婚了,两人生育了6名子女,生活幸福,携手到老。
并不是每个人都能像开普勒这样幸运,他的故事给我们留下了这样的一个迷思:一个人在交往了多少对象之后,才应该放弃“下一个更好”的想法,确定自己的理想伴侣?换句话说就是:我该什么时候收手?
这个问题,表面上是个感情问题,本质上却是个数学问题。它的系统性解决,要等到340年之后的1960s年代。
1960年2月,《科学美国人》刊登了一组数学难题,其中有一个跟开普勒相亲问题有相同本质的“经典秘书问题”:
假设有n名候选人来申请秘书岗位,你作为面试官,要挨个面试他们,并当场决定要不要。要,面试结束,不要,换下一个,不能回过头去录用被拒绝过的人。那么什么样的策略,才使最佳人选被选中的概率最大?
这个问题最好的解决方案叫做“
最优停止理论(optimal stopping theory)
”。推导过程在此不赘述,简单来说就是:考察前37%的申请人时,不要接受任何人的申请;然后,只要任何一名申请人比前面所有人选都优秀,就要毫不犹豫地选择他。
这个结论如果用在爱情上,就是:要想找到最理想的对象,你应该果断拒绝掉前37%的追求者(不管他们有多好),然后在遇到比之前37%的人更好的人选时,果断娶/嫁他,不要管后面是不是还有更好的。
以开普勒为例,他一共给自己安排了11次相亲,最大概率找到理想妻子的方法是:放弃掉前11×37%≈4位女士,然后从第5个开始,只要下一位女士比前面4个更令他心生爱慕,就马上终止相亲,跟这位女士结婚。
事实上,开普勒遇到的第5位女士,就比前4位都要好,开普勒完全被她迷住,从概率上来讲,这位女士最可能是开普勒的理想妻子,事实证明也是对的。在他相完11次亲之后,开普勒并没发现比第5位更好的,只能厚着脸皮再找回来。
按照这套理论,“结婚时机学”方法论可以总结为:
①估算出这辈子你能谈多少次恋爱,用N来表示。比如假设你从18岁就开始谈恋爱,可以谈到32岁(再拖就要被老妈吊打和以死相逼),2年谈一次,那么N就等于(32-18)/2 = 7次;
② 算出临界点 M=N×37% 。比如7×37% = 2.59 ≈ 2次
③ 执行策略:前M个恋爱对象统统放弃,后面只要遇到比前M个好的人,就定下来。在假设中,就是前2个恋人放弃,从第3个开始,只要比前2个好,就确定关系。
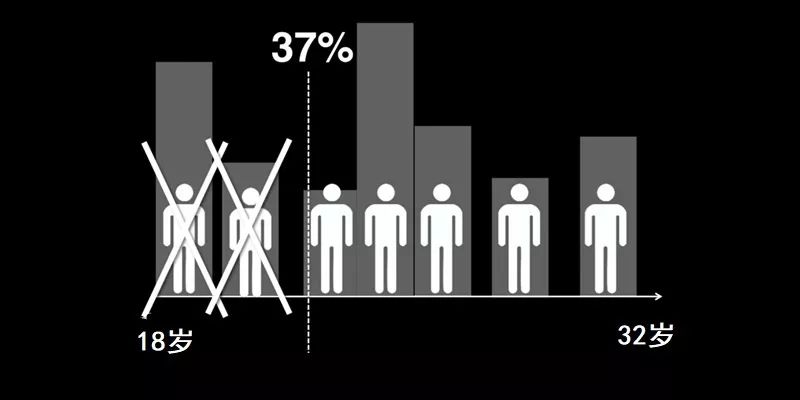
感兴趣的同学可以算一算,最大概率适合你的人,是还没出现,还是已经被你错杀了?
当然,以统计学为基础的模型,一旦用于感情生活,就会过于冰冷和生硬。虽然数字和概率要远比山盟海誓和甜言蜜语真实,但还是请读者谨慎使用。其实“最优停止理论”还可以广泛用于面试、买房、购物等,婚姻只是一个小小的应用领域。
卡内基-梅隆大学的运筹学教授迈克尔·特里克,曾经用这套方法来指导择偶,他在结束“观察期”后,很快便发现某个交往的姑娘比之前所有约会对象都优秀,符合算法为这个步骤开出的所有条件。于是果断出手,向她求婚。
妹想到,女孩干脆利落地拒绝了他。
这个悲伤的故事,可以用一段流传甚广的段子来总结:总有一天,你会遇到这样一个女孩,她温柔体贴,漂亮大方,不嫌你穷,不嫌你丑,不要钱,不要房,不要车,也不要你。
时机可以单向演算,婚姻却是双向选择。在决定出手前,一定先让自己足够优秀,否则任何模型计算出来的时机,都可能变成一场缜密的一厢情愿。
















