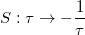正文
“群”（group）的
结构，而对称操作的复合给出了群上的
乘法运算规则
。除了乘法规则，群还应当满足其它一些简单的性质。比如说，对每个对称操作
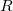，都应该能够找到另一个对称操作
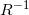，使得当我们把它们复合起来的时候，得到的结果不仅仅是一个对称操作，而且要让作用的对象完全不变。这样让作用对象完全不变的操作称为群的单位元，通常用
1
表示。因此，对群中的每个元素
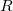都存在着一个
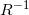使得
最后，假如我们要执行
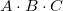这个操作，我们可以认为是要先做
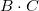, 接着做
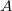（记为
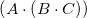），或者我们可以先做
，
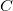
然后再做
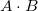（可以记成
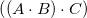），两种操作得到的结果应该完全一致。也就是说，群的乘法是满足结合律的。
我们所定义的群的概念，可以允许对称操作连续地依赖于某些变量。例如，和正三角形的情形完全不同，一个圆的对称群是连续的。我们可以把一个圆周绕着圆心转任意角度而不改变圆周的形状。在这篇文章里，我们不考虑这种元素需要用连续变量来标记的群，并且进一步假设只有有限多个群元素。因为这一条件，它们有一个十分有创意的名字——有限群
（finite groups ）
。
我们能够完全分类有限群吗？这个目标还是太大了些。但是我们至少希望能够在这个方向上迈出重要的一步。尽管完整分类宇宙当中所有可能的物质形态远远超出了我们目前的能力范围，但是随着元素周期表的确立，物理学家和化学家们成功地为我们提供了一组基本构件，能够以各种各样的方式来组成日常生活中所见的丰富多彩的物质。
粗略来说，构成对称群的“原子”是那些不能被拆成更小的群的有限群，称之为
有限单群
（finite simple groups）。令人惊叹的是，到20世纪末，数学家们成功地分类了有限单群。为了取得这一成果，上百位数学家付出了艰辛的努力，发表了超过10000页的期刊文章。有限单群的分类计划是一项史诗般的工作，有人认为，没有任何一位数学家能够完全理解整个证明，尽管数学家们至今仍然在继续化简并提炼证明中蕴含的思想。
不管怎样，数学家们已经给我们提供了一张可以用来构建对称群的“周期表”。这张周期表里有无穷多个组件，但是其中大部分在某种意义上都比较无趣：它们出现在包含无穷多个相类似的群的大家族里面。至少在比较直观的层次上，理解了其中一个基本上就意味着理解了同一系列中的所有群。这样的无穷多的家族在分类表中总共有18个。
分类表里剩下的都是一些怪胎，没法被放进那些大家族里。就像高中里的书呆子一样，它们不得不各自单独待着。这样的怪家伙一共有26个，被称为
散在群
（sporadic finite groups）。
这里面个头最大的，魔群（Monster group）
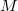，是由Griess和Fisher在上世纪70年代发现的。这是一个巨大无比的群——一共包含了大概
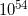个不同的对称变换。想要通过写下乘法表，然后检查乘法的自洽性来证明这个群的存在，这是没有任何指望的。“魔群”这个名字是John Conway起的，意指它庞大的体积和无与伦比的复杂性。我们在这里不准备详细描述魔群的构造，但是如果有好奇的读者想要领略一下这些构造的风味，在本文的最后一节里我们会介绍如何具体实现一个在“新月光”中出现的，相对比较简单的散在单群，
。
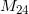大概在1978年的时候，已经有人猜测了魔群的存在，但是完整的证明还没有找到。可以确定的是，假如这个群真的存在，它不能作为对称群以任何非平凡的方式在低维空间的对象上作用（当然，它可以“平庸”地作用在任何低维对象上，包括1）。实际上，计算结果表明魔群能够作用的对象至少得是196883维。更一般地来说，魔群最小的几个
表示
的维数——也即魔群能够有不可约化的作用的空间维数——是1，196883，21296876，……
三、
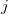函数登场
约翰·麦凯（John McKay）是思考魔群的数学家中的一员。1978年的一个夜晚，他决定休息片刻。毫无疑问，思考这样维度数以万千（甚至更多）的对称群是项相当艰苦的工作。
就像我们许多人在放松消遣时所做的一样，他翻阅了一篇近期关于数论的论文。研读这篇论文的时候，他遇到了在数论中具有重要地位的Klein
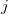函数，这一函数由如下的无穷级数展开表示（省略了常数项）：
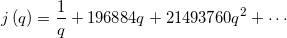
此时他的思绪还没有完全跳离魔群，他立刻意识到
。
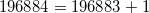也就是说，
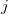函数级数展开式中第一个不平凡的系数，竟然和魔群的第一个非平凡表示的维数
惊人地接近
！
随后，他和约翰·汤普森（John Thompson，菲尔兹奖得主，群论专家）意识到，这个“巧合”竟还延续到
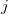函数的高阶展开系数，例如
。
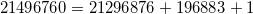从这些对数字的朴素观察中，“魔群月光”领域诞生了，其目标正是揭开和解释最大的散在单群（sporadic simple symmetry groups）与模函数（modular functions）理论（研究
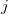函数及其“同类”）之间玄妙的联系。
让我们暂停片刻，先来了解一下模函数指的是什么。考虑一个复变量
的函数
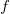，它在如下两种变量替换（下文中称它们为
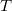变换和
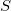变换）下函数值均不变：
