正文
1
)的可信度进行更新
(
分别见公式
3
和公式
4)
，得到它们更新的后验概率。
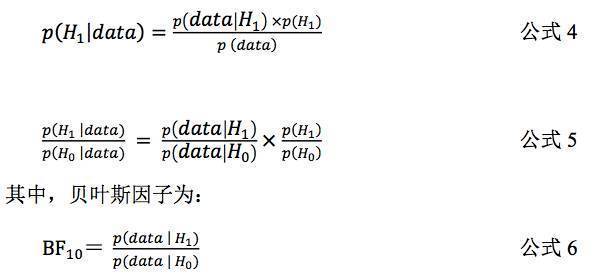
在公式
6
中，
BF
10
中下标的
1
，代表的是
H
1
，
0
代表的是
H
0
，因此，
BF
10
即代表的是
H
1
与
H
0
对比的贝叶斯因子，而
BF
01
即代表的是
H
0
与
H
1
对比的贝叶斯因子。例如，
BF
10
=
19
表示的是，在在备择假设
H
1
为真条件下出现当前数据的可能性是虚无假设
H
0
条件下出现当前 数据的可能性的
19
倍。
从贝叶斯因子的公式中可以看出，贝叶斯因子不依赖于对先验假设(
p
(
H
1
)
和
p
(
H
0
)
)。更重要的是，正是贝叶斯因子根据当前数据将先验概率更新为后验概率。
因此，
NHST
与贝叶斯因子回答了不同的问题。
NHST
试图回答“假定我们已知两个变量
的关系(如，两种条件没有差异)，出现当前观测数据的模式或者更加极端模式的概率(
p
(more extreme > observed data|H0)
)有多大”的问题;而贝叶斯因子试图回答的是，在当前数据更可 能在哪个理论模型下出现。考虑到研究者往往想知道当前数据模式条件下，
H
0
或者
H
1
为真的 概率(分别为
p
(
H
0
|data)
与
p
(
H
1
|data)
)，在假设检验中，贝叶斯因子具有一些
NHST
不具备的 优势，下一小节将对这些优势进行详细说明。
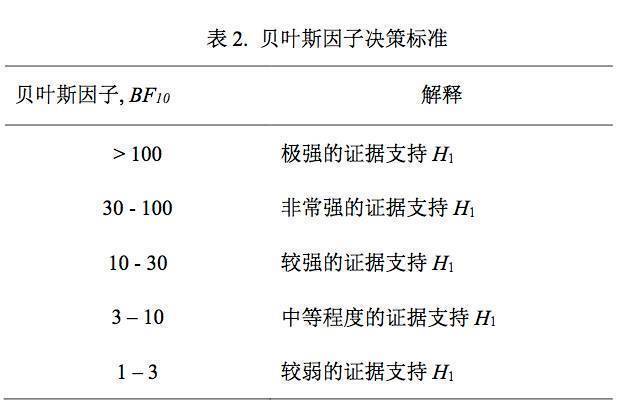
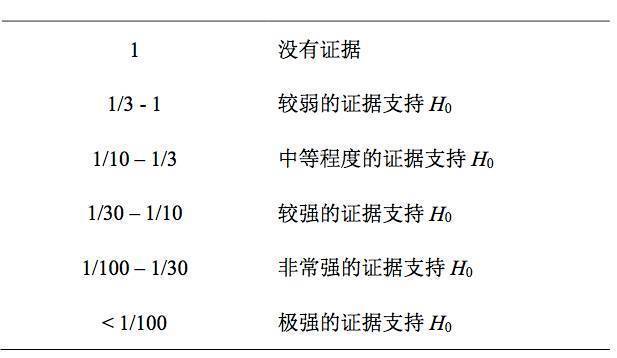
对贝叶斯因子大小的解读，在
Jeffreys (1961)
的基础上，
Wagenmakers, et al. (2017)
对贝叶斯因子的大小所代表的意义进行原则上的划分(见表
2
)。但是这个划分仅是大致参考，不能严格对应，研究者需要根据具体的研究来判断贝叶斯因子的意义。
由于贝叶斯因子中先验概率具有至关重要的作用，因此如何选择备择假设的先验分布变成 了一个非常重要的问题。其中一个较为合理的做法是，根据采用该范式的先前研究(如元分析得到的效应量)来假设备择假设的先验分布。但这种做法在很多情况下并不现实:首先根据范式的不同，效应量的可能分布不同;更重要地，由于许多研究本身具有一定的探索性，并没有先前研究结果作为指导。因此，更加常用的做法是使用一个综合的、标准化的先验。
例如，在贝叶斯
t
检验中，零假设的先验比较好确定，但是对于备择假设的先验分布应该 如何选择，则比较困难。有研究者指出，使用柯西分布(
Cauchy distribution
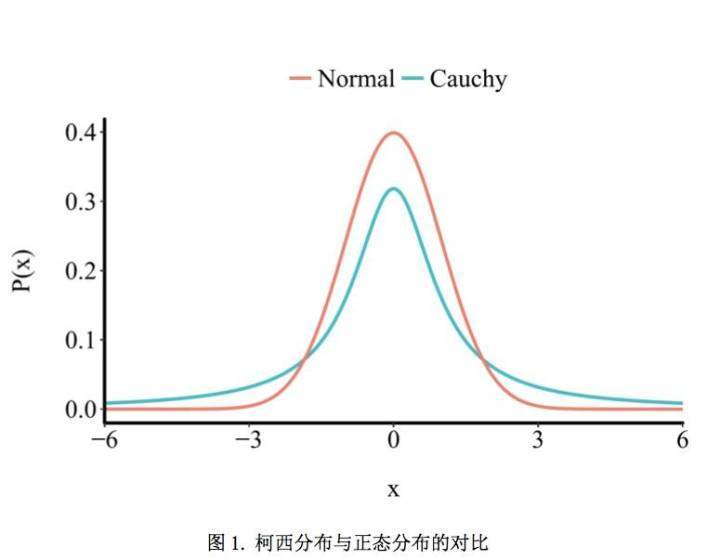
)可能是比较合理 的选择。与标准正态分布相比，柯西分布在
0
附近概率密度相对更小一些，因此其比 标准的正态允许更多较大的效应(见图
1
);而与均匀分布(即效应量在所有值上的分布完全相 同)相比，柯西分布更偏好零假设一些。因此，对于备择假设的先验分布，可以如下表示:
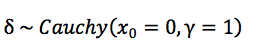
Jeffreys (1961)
最早提出在贝叶斯因子中使用柯西分布作为先验来比较两样本的问题。最近
研究者的进一步验证表明，柯西分布可以作为先验用于计算心理学常规假设检验中的贝叶斯因 子，如
t
检验、
ANOVA
和相关分析等。这些验证性的工作，为贝叶斯因子在心理学 及相关学科研究中的应用打下了基础。
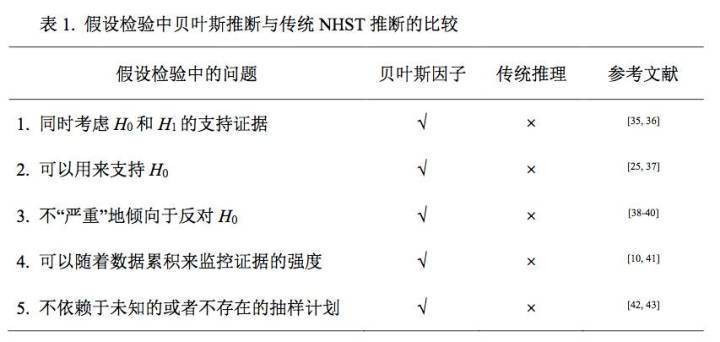
如前所述，在假设检验中，贝叶斯因子除了更加符合人们的直觉之外，还具有一些
NHST
具备的优势。这些优势可以总结为五个方面(见表
1
)。以下将从这五个方面展开。
如前所述，贝叶斯因子的计算同时考虑
H
0
和
H
1
，并根据全部现有数据对
H
0
和
H
1
为真的 先验概率进行更新，在此基础之上，比较在当前数据下哪个理论模型(
H
0
和
H
1
)更合理。这种思路与
NHST
不同:在
NHST
框架之下，计算
p
值需要假定
H
0
为真，而对
H
1
不做任何假
设，因此
p
值与
H
1
无关;
NHST
的逻辑是，如果
H
0
为真，观察到当前数据出现的概率非常小，则拒绝
H
0
，接受
H
1
;这种情况下，
NHST
忽略了一种可能性:当前数据下，
H
1
为真的概率与
H
0
为真的概率相当或者更小。例如，在
Bem (2011)
中，
H
0
是被试的反应不受到未来出现 刺激的影响，
H
1
是未来出现的刺激会影响到被试当前反应，即被试能够“预知”尚未出现的刺 激。虽然采用
NHST
的逻辑
Bem (2011)
得到了
p
< 0.05
的结果，即
H
0
为真时，得到当前数据 的概率(
p
(
data
|H0)
)很低，因此作者选择拒绝
H
0
而接受
H
1
，认为被试能够预知未来出现的刺 激。然而，研究者更关心的是，根据当前数据，某个模型
/
假设(如
H
1
)为真的概率(
p
(
H
1
|
data
)
)， 而非零假设
H
0
为真时得到当前数据的概率(
p
(
data
|
H
0
)
)。考虑到先验知识告诉我们
H
1
本身为 真的概率可能非常低，在当前数据模式下，
H
1
为真的可能性
p
(
H
1
|
data
)
极可能比
H
0
为真的可 能性
p
(
H
0
|
data
)
更低。
此外，
p
值等于在
H
0
为真的情况下，多次重复实验观察到与当前数据一样极端或者更加极端结果的概率
，即
p
值是假定
H
0
为真时概率分布的尾端面积的积分值。因此，对
p
值的理 解需要假定存在着比当前数据更加极端的数据模式，而人们在直觉上并不太擅长做出这种假定， 常常会带来对
p
值的误解。
因此，由于贝叶斯因子分别量化了当前数据对
H
0
和
H
1
的支持强度，对
H
0
