正文
一、客户购买行为随机模型中隐藏着哪些秘密?
随机模型除了显示购买频率概率、平均金额概率的密度分配,还隐藏着购买频率、平均金额的状态移转期望值和概率这两个秘密,等待被揭示。
揭秘后,您就更加理解用必要长度和宽度的样本数据建立起一套牢固、可靠随机模型的重要意义,样本越大,客户价值推测结果就越接近即将发生的事情。
【客户随机购买行为的六个基本假设】
-
假设一:假设客户随机购买频率和随机购买金额两个不同的行为纬度互相独立,不具有相关性。
-
假设二:假设客户的购买状态移转行为符合马可夫链的假设,这表示客户下一期购买状态发生的机率只和上一期的购买状态有关。
-
假设三:假设个别客户购买频率为卜松分配(Poisson Distribution)。
-
假设四:考虑客户的异质性,假设上述个别客户单位时间平均购买次数服从伽玛分配(Gamma Distribution)。
-
假设五:假设个别客户有购买行为的各期平均单次购买金额为伽玛分配(Gamma Distribution)。
-
假设六:考虑客户的异质性,假设上述各期平均单次购买金额又符合另一个伽玛分配(Gamma Distribution)。
1、观察随机模型
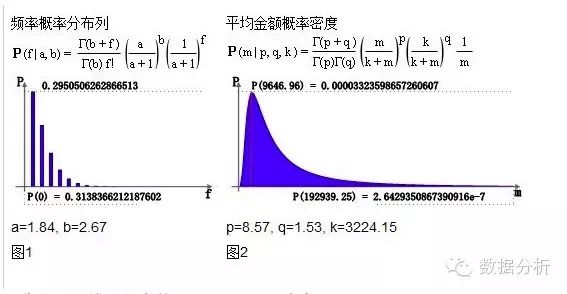
曲线形状均由其参数a、b、p、q、k决定。
频率概率分布列符合负二项分配,参数a、b由客户的平均购买频率计算出来。假设有一组样本,对应n家成交客户,fi(i = 1, 2 … n)【样本长度为n】表示每家客户的平均购买次数,通过最大概似估计法可求得a、b,并且可求得平均频率 = b/a。频率模型为离散函数,f>0,频率平均值=ceil(b/a)=ceil(2.67/1.84)=2。示例的无成交概率分布列P(0)≈31%,意味着其余有成交概率分布列之和ΣP(i)≈69%,其中P(1)≈30%(峰值),P(2)≈19%,P(3)≈10%。
平均金额概率密度符合伽玛-伽玛分配,参数p、q、k由客户的平均购买金额计算出来。假设共有n家客户【样本长度为n】,且每家客户有发生购买行为的期数分别为hk(k=1, 2 … n)【样本宽度分别为hk】,每家客户有发生购买行为期间的该期平均单次购买金额为mi,j(i=1, 2, … n, j=1, 2, … hi),通过最大概似估计法可求得p、q、k,并且可求得对应峰值概率的平均金额 = (p-1)/(q+1)*k。平均金额m的概率密度分配为连续函数,m>0,p、q为形状参数,k为尺度参数。示例的峰值概率密度位于m=9646.96,P(9646.96)=0.00003323598657260607。
从上面随机模型中您已能初步观察到购买频率、平均金额的概率分布情况。
2、推导购买频率、平均金额移转期望值
以平均金额为例,观察以下图形:
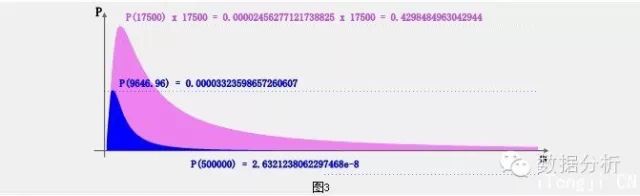
蓝色的就是平均金额概率密度曲线,紫色的是m轴每个mi坐标乘以对应蓝色概率密度pi得到的新曲线。换句话说,紫色包络线上每个点的值都是蓝色包络线对应点的mi倍。
在上图任意位置mi作条垂线,垂线至m=500,000.00(假设此为历史最大平均金额)之间,紫色面积除以蓝色面积,结果就是mi的状态移转期望值。可对m设定一些刻度,如0.01、1,000.00、10,000.00、100,000.00、200,000.00、300,000.00、400,000.00,即可得到这些刻度的对应的平均金额移转期望值。
用积分表达式描述就是:平均金额移转期望值 = ∫紫色曲线函数dm / ∫蓝色曲线函数dm,积分区间由mi到500,000.00。
购买频率移转期望值也类似,只是频率概率为离散函数。
3、推导购买频率、平均金额移转概率

















